Радиус окружности

Радиус окружности, определение

Окружность — это геометрическая фигура, которая состоит из всех точек плоскости, находящихся на одинаковом расстоянии от определенной фиксированной точки, называемой центром окружности. Окружность состоит из бесконечного числа точек и является замкнутой кривой.

Радиус окружности — это отрезок, который соединяет центр окружности с любой точкой на ее окружности. Радиус является постоянной величиной для конкретной окружности и половиной ее диаметра, самого длинного отрезка, который можно провести внутри окружности. 

Эта величина — одна из ключевых в геометрии, так как позволяет находить параметры других геометрических фигур, вписанных или описанных вокруг окружности. Радиус входит в формулы для вычисления длины окружности, площади круга, а также является важной составляющей формул для нахождения параметров вписанных или описанных фигур, таких как треугольники и квадраты. Традиционно обозначается буквой r. 

Формула радиуса окружности

Через длину окружности

Когда известна длина окружности, радиус можно найти, воспользовавшись формулой длины окружности. Длина окружности L определяется как произведение удвоенного радиуса на число π (π ≈ 3,14): L = 2πr

где:

• L — длина окружности;
• π — математическая константа;
• r — радиус окружности.

Исходя из этой формулы, радиус r можно выразить следующим образом:

Таким образом, чтобы найти радиус, нужно разделить длину окружности на удвоенное значение числа π. 

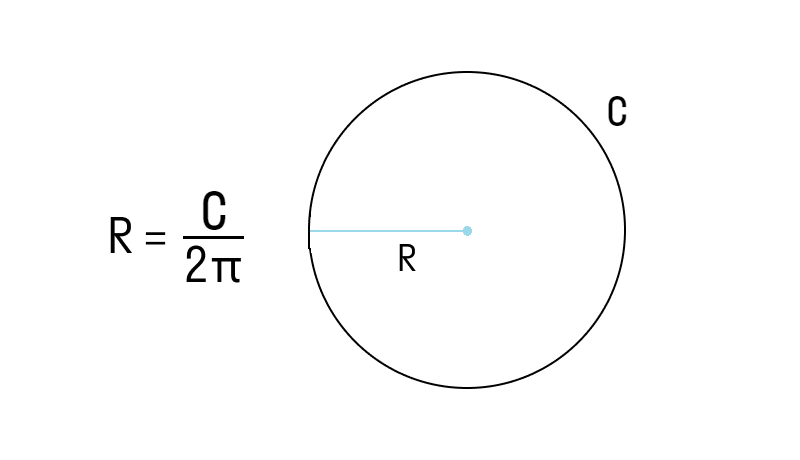
Если известна длина окружности

Через диаметр окружности

Диаметр окружности, обозначаемый буквой D, представляет собой расстояние между двумя точками окружности, проходящее через ее центр. Диаметр окружности всегда в два раза больше радиуса:

D=2rD

Исходя из этой зависимости, радиус можно найти по формуле: r = D/2

Это один из самых простых способов нахождения радиуса, так как диаметр часто измерить легче, чем другие параметры окружности. В данной формуле:

• D — диаметр окружности;
• r — радиус окружности.

Если известен диаметр окружности, радиус можно получить делением диаметра пополам.

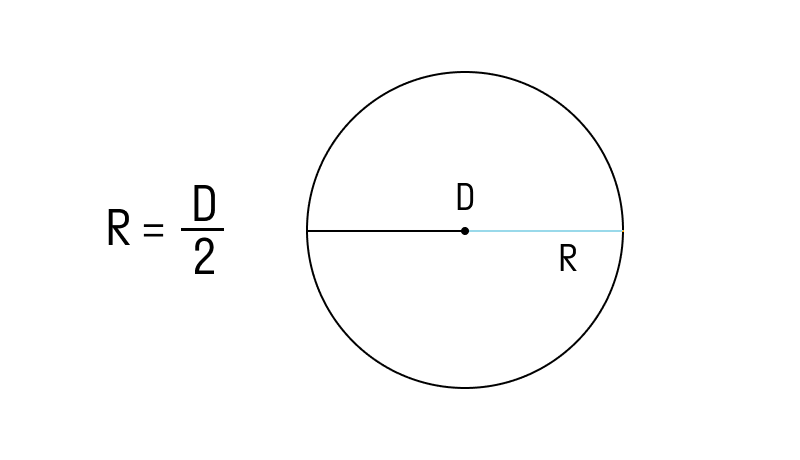
Если известен диаметр окружности

Через площадь круга

Площадь круга S также можно использовать для нахождения радиуса. Формула площади круга выводится из зависимости площади от квадрата радиуса:

где:

• S — площадь круга;
• r — радиус окружности;
• π — математическая константа.

Если известна площадь круга, радиус можно найти, преобразовав формулу следующим образом:

1. Разделить площадь круга на π: 

1. Извлечь квадратный корень из полученного значения: 

Этот метод применим, когда известна площадь круга, но неизвестна его длина или диаметр.

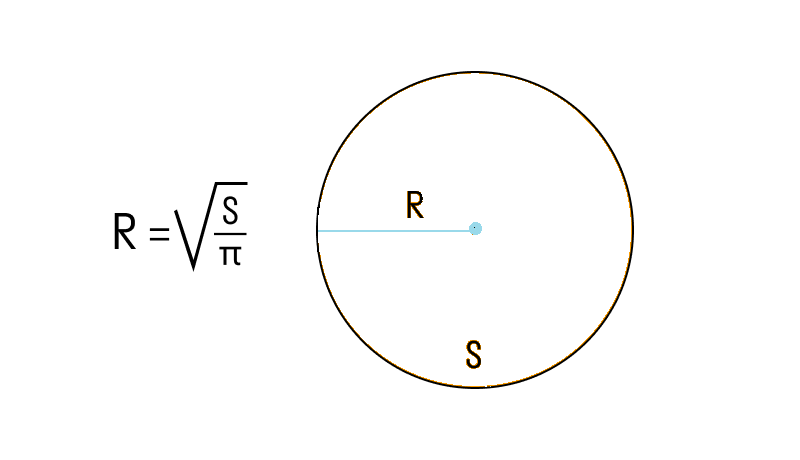
Если известна площадь круга

Через диагональ вписанного прямоугольника

Если прямоугольник вписан в окружность, то его диагональ равна диаметру окружности. Это связано с тем, что в такой конфигурации диагональ проходит через центр окружности. Пусть d — длина диагонали прямоугольника, тогда радиус окружности можно найти как: r = d/2

где:

• d — диагональ прямоугольника;
• r — радиус окружности.

Таким образом, радиус окружности равен половине длины диагонали вписанного прямоугольника. Этот способ удобен, когда известны параметры вписанного прямоугольника, но не окружности напрямую.

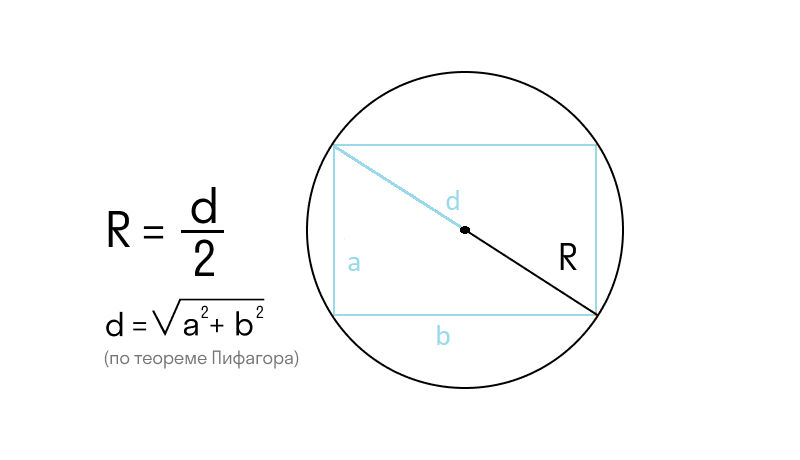
Если известна диагональ вписанного прямоугольника 

Через сторону описанного квадрата

Если окружность описана вокруг квадрата, то радиус окружности будет равен половине длины стороны квадрата. В этой ситуации сторона квадрата служит диаметром окружности, и радиус можно выразить так: r = a/2

где:

• a — длина стороны квадрата;
• r — радиус окружности.

Этот метод удобен, если известна сторона квадрата, описанного вокруг окружности. Он часто используется в задачах на построение и анализ фигур, когда радиус окружности зависит от размеров описанного квадрата.

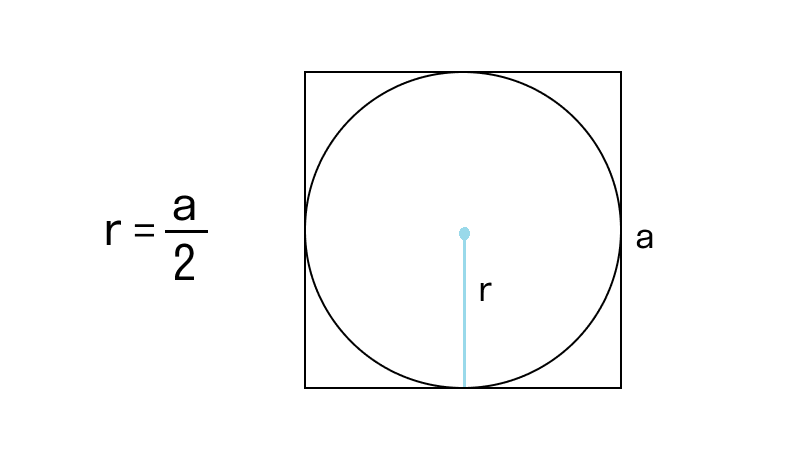
Если известна сторона описанного квадрата 

Через сторону и площадь вписанного треугольника

Для нахождения радиуса окружности, вписанной в треугольник, важно учитывать тип треугольника. Вписанная окружность касается всех трех сторон треугольника, и ее радиус может быть выражен через сторону и площадь треугольника.

1. Для прямоугольного треугольника радиус вписанной окружности r можно найти как: r = (a + b — c) / 2
   

где a и b — катеты треугольника, а c — его гипотенуза.

1. Для равностороннего треугольника с длиной стороны a:
   

Этот метод позволяет найти радиус, когда известны размеры сторон и тип треугольника, в который вписана окружность.

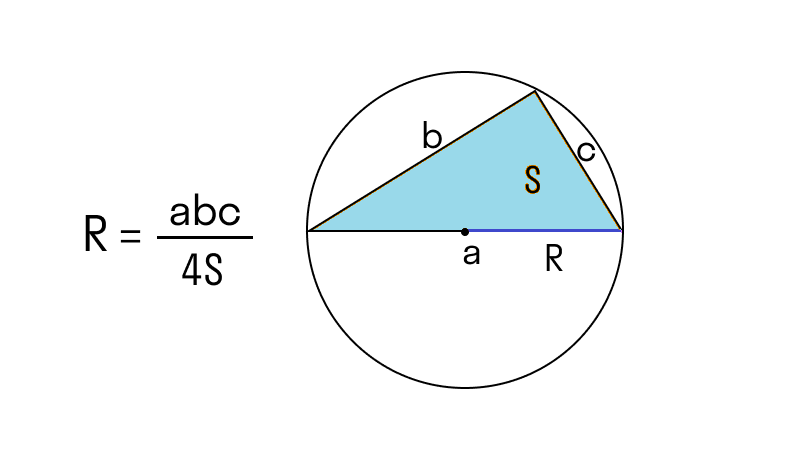
Если известна площадь вписанного треугольника 

Через площадь и полупериметр описанного треугольника

Если окружность описана вокруг треугольника, радиус можно выразить через площадь S и полупериметр p треугольника. Полупериметр — это половина суммы длин всех сторон треугольника: p = (a + b +c) / 2

где a, b и c — длины сторон треугольника.

Для нахождения радиуса описанной окружности r используется формула: r = S / p

где:

• S — площадь треугольника;
• p — полупериметр треугольника.

Такой подход применяется в задачах, где известны площадь и размеры треугольника, а требуется определить радиус окружности, описанной вокруг него.
 

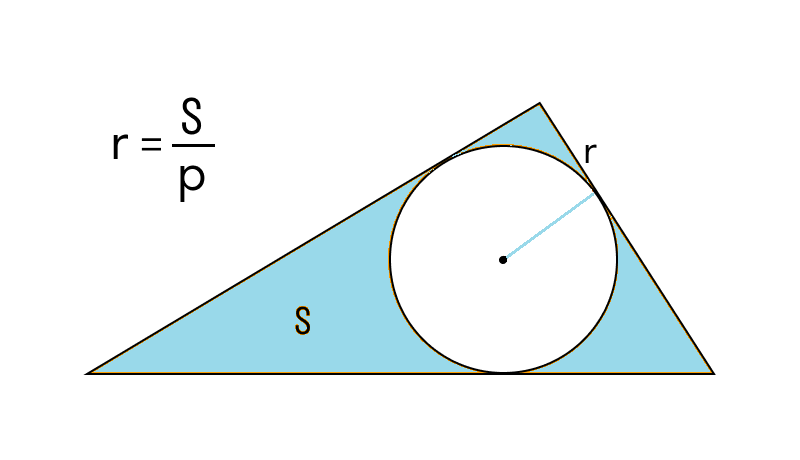
Если известна площадь и полупериметр описанного треугольника