Гипербола, формула

Что такое гипербола?

Гипербола — это кривая второго порядка, задаваемая каноническим уравнением вида  

. 

a и b — параметры, определяющие форму гиперболы. 

График гиперболы состоит из двух ветвей, удаляющихся друг от друга и центровой симметрии. В отличие от параболы, которая имеет только одну ветвь, гипербола всегда состоит из двух симметричных частей.

Простейший пример гиперболической функции:

Это уравнение описывает зависимость одной переменной от другой таким образом, что при увеличении значения x значение y уменьшается, и наоборот, то есть x и y находятся в обратной пропорциональности. Этот тип зависимости часто встречается в физических и экономических моделях, где требуется описать уменьшение величины одной переменной при росте другой.

Функция гиперболы

Функция гиперболы обычно представлена в виде:

В этом случае функция определена для всех действительных чисел, кроме нуля, так как деление на ноль не имеет математического смысла. График гиперболической функции включает асимптоты — линии, к которым приближается график, но не пересекает их. Для функции ​ такие асимптоты — это оси x и y.

График гиперболической функции можно построить, начав с выбора множества действительных чисел, подстановки их в уравнение и построения точек на координатной плоскости. Анализ поведения функции показывает, что при значение y стремится к нулю. Однако, когда x стремится к нулю слева или справа, y стремится к бесконечности.

Свойства 

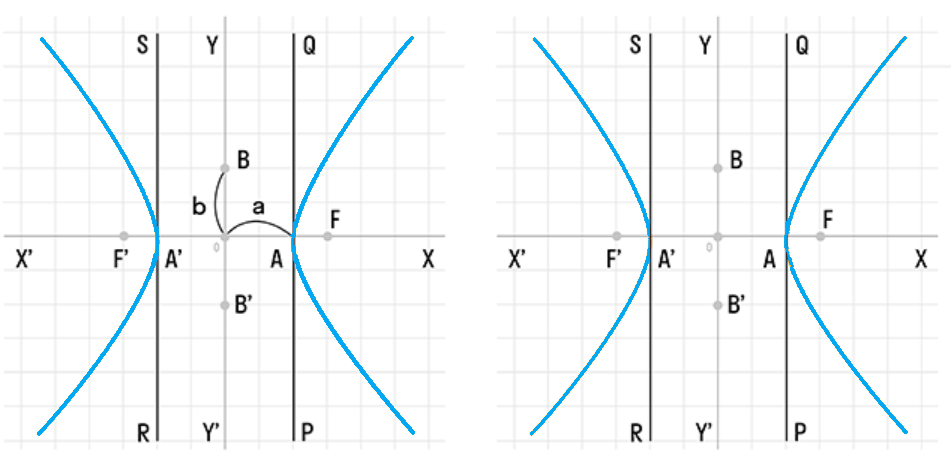
Гиперболы обладают рядом уникальных свойств:

1. Обратная пропорциональность. В случае функции вида 

 ​ 

переменные x и y находятся в обратной зависимости: когда одна увеличивается, другая уменьшается.

1. Симметрия. Гипербола симметрична относительно начала координат, так как изменение знака x или y приводит к зеркальному отображению ветвей.
2. Асимптотические линии. График гиперболы имеет асимптоты — прямые, к которым график неограниченно приближается, но не пересекает. В случае простейшей функции

это оси x и y.

Особенности

Гипербола отличается от других кривых второго порядка, таких как парабола и эллипс. Основные особенности заключаются в следующем:

Две ветви графика. В отличие от параболы, которая имеет только одну ветвь, гипербола состоит из двух отдельных ветвей, каждая из которых является отражением другой относительно начала координат. Это свойство делает гиперболу особенно интересной с точки зрения симметрии, поскольку ее ветви никогда не пересекаются, но всегда стремятся к асимптотам — линиям, к которым график приближается, но не достигает.

Применимость в различных областях. Гипербола встречается в реальной жизни в ряде научных и практических контекстов. Например, в физике законы, описывающие гравитацию, часто связаны с гиперболическими функциями, так как сила притяжения уменьшается обратно пропорционально квадрату расстояния. В астрономии гиперболические орбиты могут описывать движение комет и других небесных тел. Кроме того, в экономике гипербола используется для моделирования различных зависимостей, например, спроса и предложения.

Связь с гиперболическими функциями. Гиперболические функции, такие как гиперболический синус и гиперболический косинуc, непосредственно связаны с гиперболами и используются для описания изменений в системах, имеющих определенные математические характеристики. Эти функции являются аналогами тригонометрических функций, применяемых для работы с кругами, но они ориентированы на гиперболы и обеспечивают глубокое понимание поведения систем, которые могут быть описаны с помощью гиперболической геометрии.