Объем шара

Что такое объем шара в геометрии

Шар в геометрии — это множество всех точек, расположенных на заданном расстоянии (радиусе) от одной центральной точки (центра). 

Как и любое трехмерное тело, шар характеризуется несколькими параметрами, одним из которых является объем — это величина, показывающая, какое пространство занимает шар. С практической точки зрения объем отражает количество вещества (например, воздуха или воды), которое может поместиться внутри шара.

Объем измеряется в кубических единицах, таких как кубические метры (м³). Помимо них, в различных областях применяются литры, баррели и галлоны. В математических формулах объем обозначается латинской буквой V (volume).

Объем шара — это величина, которая показывает, какое пространство занимает шар в трехмерном пространстве. Формула для вычисления объема шара связана с радиусом, диаметром или площадью его поверхности. Понимание объема шара важно как в математике, так и в других сферах: например, в физике, инженерном деле, 3d-моделировании и астрономии. В физике его используют для расчета плотности, когда масса делится на объем, а также для определения характеристик вращающихся тел и в аэродинамике. В инженерии объем помогает оценить вместимость сферических резервуаров и других объектов. В астрономии его используют для расчета объемов планет, звезд и других сферических объектов.

Полезная информация

1. Первым объем шара вычислил Архимед в III веке до нашей эры. Он также установил соотношение между объемами цилиндра и вписанного в него шара.
2. Для вычисления объема шара используется математическая константа π, значение которой приблизительно равно 3,14159. В большинстве расчетов ее округляют до 3,14.
3. В школьной программе рассматривается трехмерный шар, однако в математике существует определение шара для пространств любой размерности n.

Как найти объем шара

Для расчета объема шара используются несколько формул, каждая из которых зависит от доступных данных. —

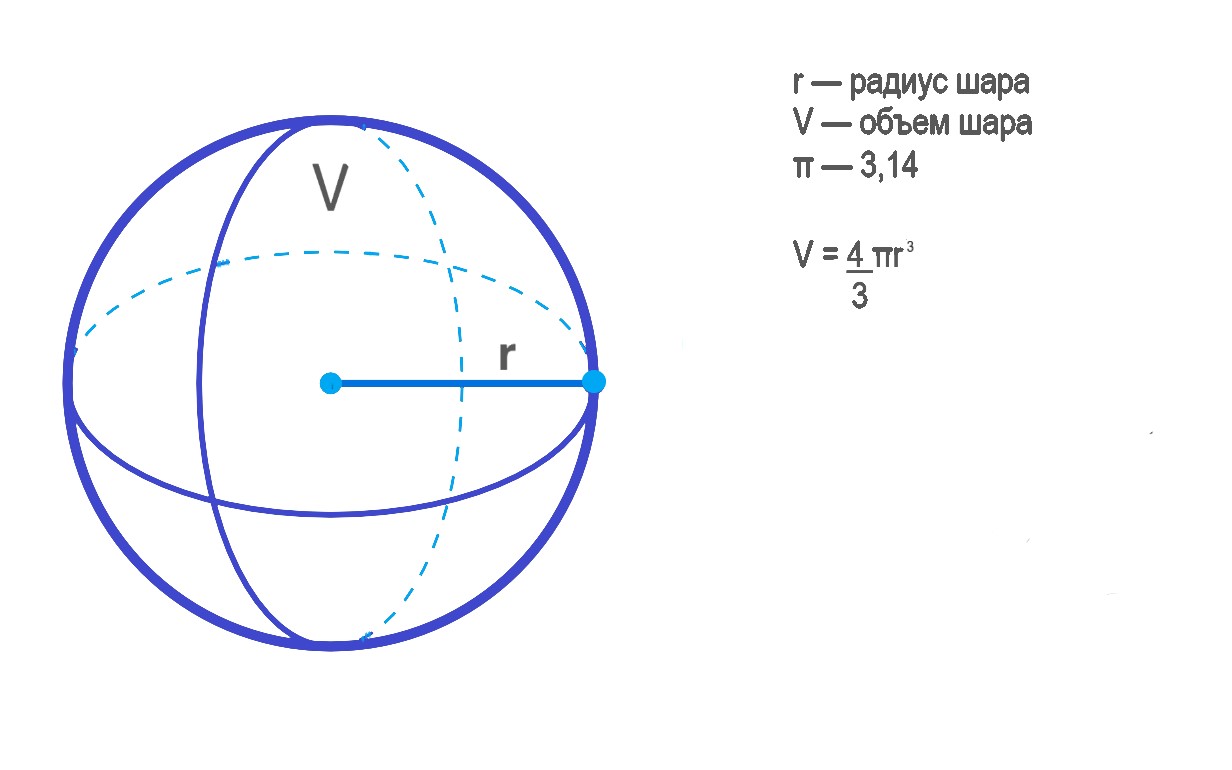
Формула через радиус

Основная формула для вычисления объема шара выглядит так: V 

=4/3 π r3

где r — радиус шара.

Пример.

Найдем объем шара радиусом r = 5 см.

Объем шара через радиус

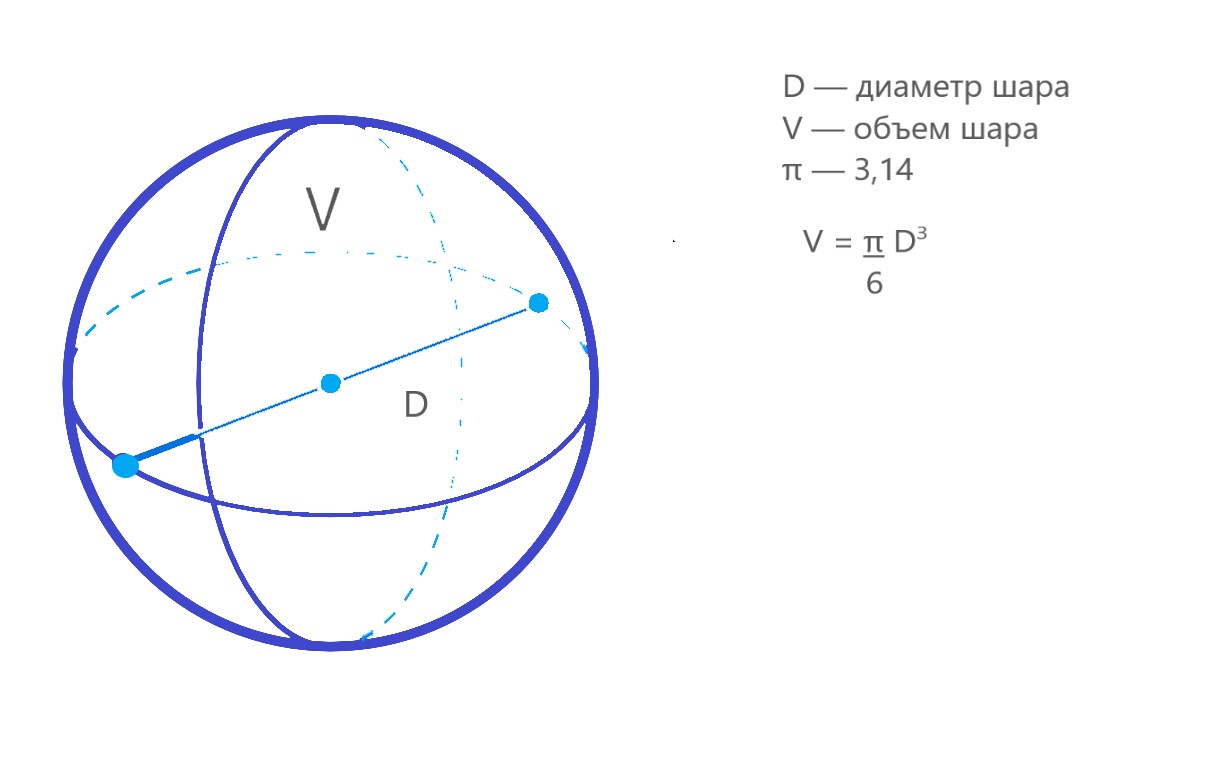
Формула через диаметр

Поскольку диаметр d шара связан с радиусом через соотношение d = 2r,

формулу объема можно записать через диаметр: V=π/6D3

Пример.

Рассчитаем объем шара с диаметром d = 10 см:

Объем шара через диаметр

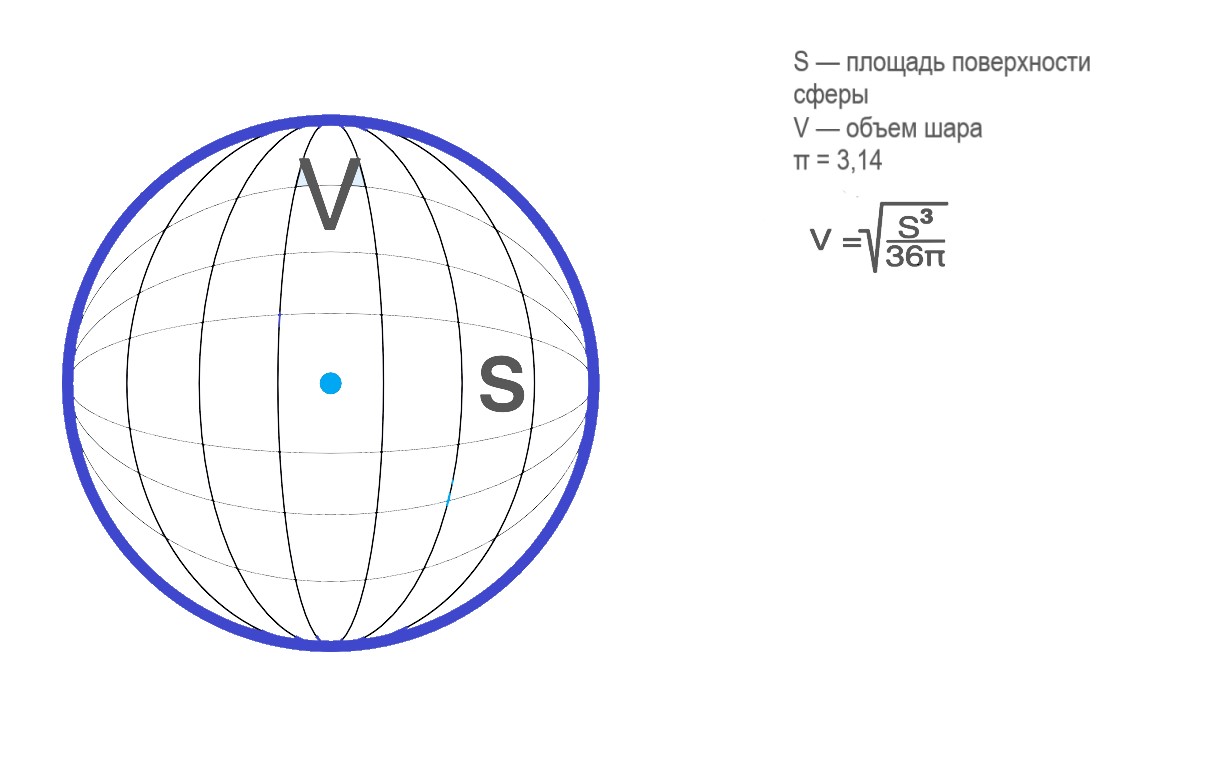
Формула через площадь поверхности

Сечение шара плоскостью, которое проходит через центр шара, называется большим кругом.

Для упрощения часто рисуют большой круг шара.

Площадь поверхности шара, или сферы, вычисляют по формуле:

где R — это радиус шара.

Объем шара вычисляют по формуле: 

где R — это радиус шара.

Объем шара через площадь поверхности

Метод Архимеда для вычисления объема шара

Метод Архимеда для вычисления объема шара стал важным достижением в математике. Архимед, известный своими работами в области геометрии и механики, в III в. до н. э. предложил способ нахождения объема шара, который основывался на его связи с цилиндром.

Архимед доказал, что объем шара равен двум третям объема цилиндра, который описан вокруг этого шара. Такой цилиндр имеет тот же радиус, что и шар, а высота цилиндра равна диаметру шара. Таким образом, объем шара можно рассчитать, зная объем цилиндра, который его ограничивает.

Для цилиндра с радиусом r и высотой h = 2r:

Тогда объем шара:

Этот метод продемонстрировал связь между разными геометрическими фигурами, что стало важным этапом в развитии математики.