Периметр прямоугольника

Что такое периметр прямоугольника?

Прямоугольник — это геометрическая фигура, которая имеет четыре стороны и четыре угла. Все углы в прямоугольнике прямые, то есть равны 90 градусам. Противоположные стороны прямоугольника равны и параллельны друг другу. 

Периметр прямоугольника — это сумма длин всех его сторон. Этот параметр помогает понять, насколько велика «граница» прямоугольника. В математике обычно обозначается буквой P. 

Периметр может измеряться в различных единицах, таких как:

• миллиметры (мм)
• сантиметры (см)
• дециметры (дм)
• метры (м)
• километры (км) и другие

Как найти периметр прямоугольника?

Вычисление периметра прямоугольника — это одна из базовых задач школьной программы по математике, изучается в начальной школе.

Примеры задач для второго класса на нахождение периметра 

Задача 1. Найдите периметр прямоугольника, если его длина 6 см, а ширина 3 см. Решение. Периметр прямоугольника: P = 2(a + b).

Подставляем значения:

P = 2(6 + 3) = 2 × 9 = 18 см

Задача 2. Периметр прямоугольника 24 см, а одна из сторон равна 8 см. Найдите длину другой стороны. 

Решение. Из формулы для периметра P = 2(a + b) имеем:

24 = 2(a + 8)

Разделим обе части на 2:

12 = a + 8

Вычитаем 8:

a = 4 см

Длина другой стороны равна 4 см.

Как найти периметр прямоугольника, если известны другие параметры

Через две стороны

Для нахождения периметра прямоугольника через две его стороны используется следующая формула:

P = 2(a + b)

Здесь a и b — длина и ширина прямоугольника, то есть его две соседние стороны. 

Через четыре стороны

В случае, если нужно вычислить периметр прямоугольника через все четыре его стороны, можно использовать формулу:

P = a + b + c + d

где a, b, c и d — это длины сторон прямоугольника.

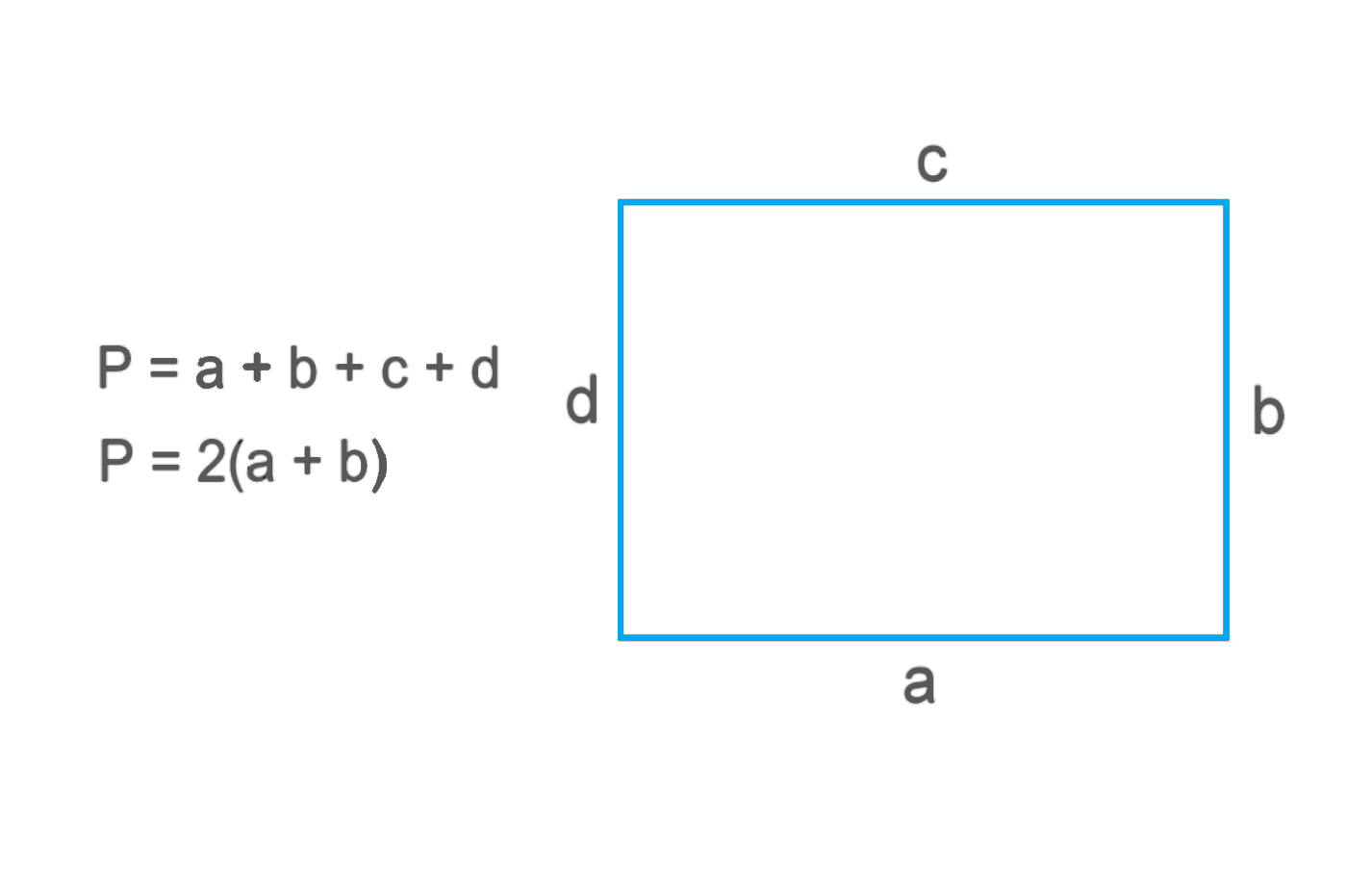
Найти периметр прямоугольника можно по сторонам

Через сторону и площадь

Если известна площадь прямоугольника и длина одной его стороны, то периметр можно найти, используя формулу для площади прямоугольника:

S = a × b, 

где S — площадь прямоугольника, a — длина одной стороны, а b — другая сторона. 

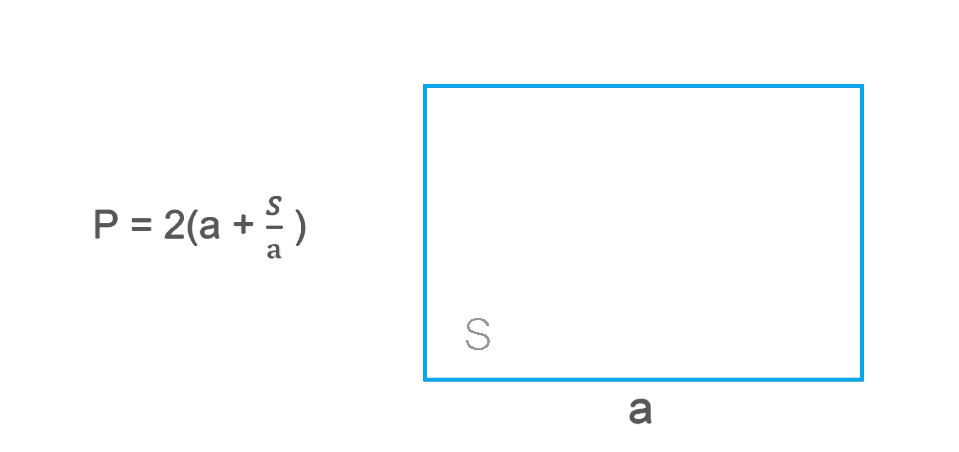
Найти периметр можно через сторону и площадь

Через сторону и диагональ

Если известны длина одной стороны прямоугольника и длина его диагонали, можно использовать теорему Пифагора для вычисления второй стороны. Согласно этой теореме, для прямоугольного треугольника квадрат гипотенузы равен сумме квадратов катетов (в нашем случае катеты — это стороны прямоугольника, а гипотенуза — диагональ).

где d — диагональ прямоугольника, a — длина одной стороны, а b — длина другой стороны. 

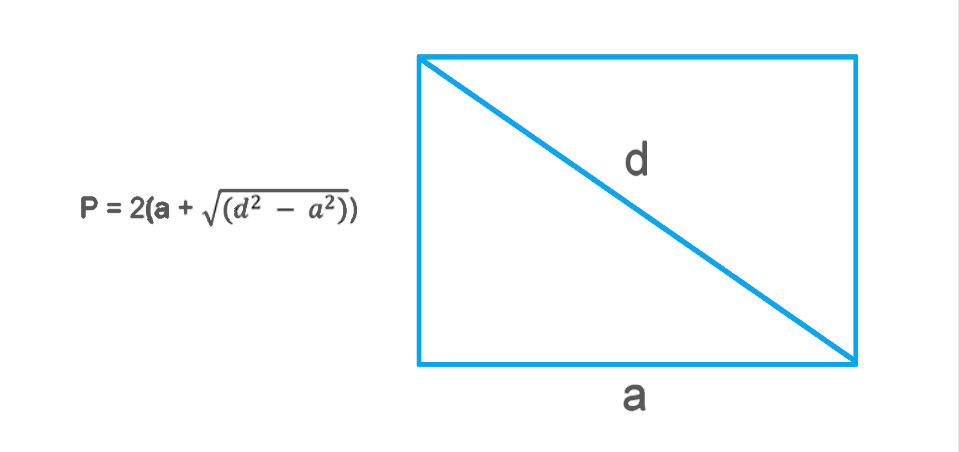
Найти периметр можно через сторону и диагональ

Через сторону и радиус описанной окружности

Прямоугольник можно вписать в окружность так, что эта окружность будет касаться всех его вершин. Радиус описанной окружности равен половине диагонали прямоугольника. Это свойство прямоугольника позволяет нам найти периметр через радиус описанной окружности.

Если r — радиус описанной окружности, то диагональ прямоугольника будет равна 2r. Теперь, зная диагональ и одну из сторон, можно использовать теорему Пифагора, чтобы найти вторую сторону. Вспомним, что для прямоугольного треугольника:

где d — диагональ, a и b — стороны прямоугольника. Зная радиус окружности, можно найти диагональ: d = 2r, а затем использовать ее для вычисления периметра через теорему Пифагора и стандартную формулу для периметра.

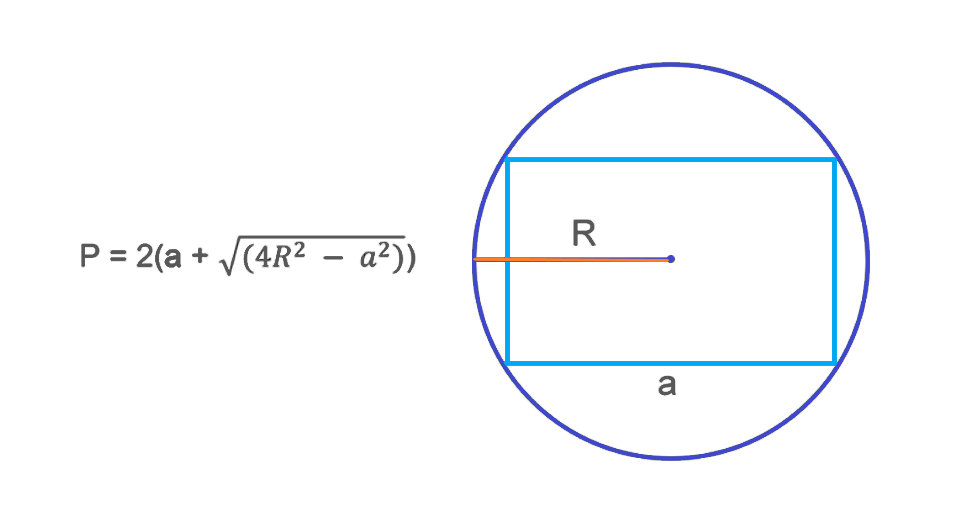
Найти периметр можно по стороне прямоугольника и окружности