Формула тангенса
Содержание
ПоказатьСкрыть
Содержание
Что такое тангенс?
Тангенс — это тригонометрическая функция, определяемая как отношение противолежащего катета к прилежащему катету прямоугольного треугольника. Другими словами, тангенс угла в прямоугольном треугольнике равен отношению противолежащей стороны к прилежащей стороне этого угла.
Тангенс является одной из основных тригонометрических функций и широко используется в математике, физике, инженерии и других научных областях для работы с углами и прямоугольными треугольниками.
В геометрии записываются сокращенно на латинском языке как tg.
Как найти тангенс: тангенс острого угла в прямоугольном треугольнике равен отношению противолежащего катета к прилежащему катету, то есть tg α = sin α / cos α.
Основные особенности и свойства тангенса:
- Определение через синус и косинус. Тангенс угла определяется как отношение синуса к косинусу этого угла
- Периодичность. Тангенс является периодической функцией с периодом π.
- Асимптоты. Тангенс имеет вертикальные асимптоты в точках, где косинус равен нулю.
- Область определения. Область определения тангенса — все действительные числа, кроме точек, где косинус равен нулю
- Область значений. Область значений тангенса — вся числовая прямая
- Симметрия. Тангенс является нечетной функцией
- Монтоность. Тангенс является монотонно возрастающей функцией на каждом из интервалов
- Преобразование углов. При изменении угла на π\piπ значение тангенса не изменяется, что отражает его периодичность.
График тангенса
Функция тангенса обозначается как y = tg (x).
График в общем виде выглядит следующим образом:
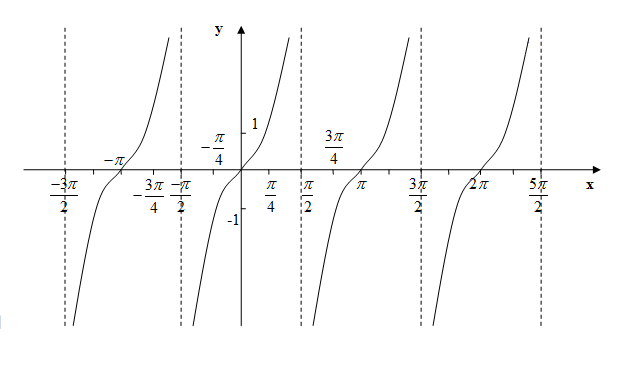
Свойства тангенса
| Симметричность | tg (-α) = -tg α |
| Симметричность | tg (90°- α) = ctg α |
| Тригонометрические тождества | tg α = sin α / cos α |
| tg α = 1 / ctg α | |
| Тангенс двойного угла | tg 2α = 2 tg α / (1 - tg2α) |
| Тангенс суммы углов | tg (α+β) = (tg α + tg β) / (1 - tg α tg β) |
| Тангенс разности углов | tg (α-β) = (tg α - tg β) / (1 + tg α tg β) |
| Сумма тангенсов | tg α + tg β = sin (α + β) / cos α cos β |
| Разность тангенсов | tg α - tg β = sin (α - β) / cos α cos β |
| Производная тангенса | tg' x = 1 / cos2 (x) |
| Интеграл тангенса | ∫ tg x dx = -ln |cos x| + C |
| Формула Эйлера | tg x = (eix - e-ix) / i(eix + e-ix) |
Формула расчета тангенса
Тангенс угла
Тангенс угла можно вычислить как отношение противолежащего катета к прилежащему катету прямоугольного треугольника при заданном угле.
Тангенс угла 90 градусов не определен, потому что в прямоугольном треугольнике, прямой угол находится между катетом, длина которого равна 0 (прилежащий катет), и гипотенузой, длина которой также равна 0 (противолежащий катет).
Поскольку тангенс угла определяется как отношение противолежащего катета к прилежащему катету в прямоугольном треугольнике. Поэтому в случае угла 90 градусов, когда и прилежащий катет, и противолежащий катет равны 0, отношение этих сторон не определено. Таким образом, тангенс угла 90 градусов является неопределенным значением в тригонометрии.
Тангенс числа
Тангенс числа вычисляется как отношение синуса числа к косинусу числа
Тангенс 0
Тангенс угла 0 равен 0, так как при угле равном 0 гипотенуза тоже равна 0, и тангенс вычисляется как отношение противолежащего (в данном случае - 0) катета к прилежащему (также 0) катету в прямоугольном треугольнике, что даёт результат 0.
Пример задачи
1. Пример 1:
Вычислите тангенс угла, если синус этого угла равен ( frac{3}{5} ) и косинус равен ( frac{4}{5} ).
Решение:
По определению тангенса: ( tan(theta) = frac{sin(theta)}{cos(theta)} ).
Заменяем данные значения: ( tan(theta) = frac{frac{3}{5}}{frac{4}{5}} = frac{3}{4} ).
Ответ: Тангенс этого угла равен ( frac{3}{4} ).
2. Пример 2:
Найдите угол, если его тангенс равен (-frac{1}{3}).
Решение:
Используем определение тангенса: ( tan(theta) = frac{sin(theta)}{cos(theta)} ).
Так как (-frac{1}{3} = frac{-1}{3}), то мы ищем, в каком угле синус равен -1, а косинус равен 3.
Это угол ( theta = -frac{pi}{6} ) (или -30 градусов).
Ответ: Угол, с тангенсом -1/3, равен -30 градусам.



