Теория вероятности

Что такое теория вероятностей

Теория вероятностей (или тервер) — это раздел математики, который изучает случайные события и помогает оценить, насколько вероятен тот или иной исход. Если результат нельзя предсказать точно, теория вероятностей дает способ рассчитать вероятность. Например, при подбрасывании монеты нельзя заранее сказать, что выпадет, но можно с уверенностью утверждать: вероятность орла и решки для симметричной монеты — по 50%.

Применение теории вероятностей — не только в математике. Ее используют в медицине, чтобы оценить риск заболевания, в страховании — чтобы рассчитать страховую премию, в маркетинге — чтобы спрогнозировать поведение аудитории. В Data Science на основе вероятностей строят алгоритмы, которые распознают лица, предсказывают спрос, подбирают рекламу. Даже в повседневной жизни мы интуитивно оцениваем вероятность случайного события: например, решаем, стоит ли брать зонт, если прогноз обещает дождь.

Теория вероятностей нужна, чтобы принимать взвешенные решения в условиях неопределенности. Она переводит случайность в числа — и делает ее управляемой.

Основные понятия в теории вероятностей

Чтобы понимать, как работает теория вероятностей, нужно знать несколько базовых терминов. Эти основные понятия теории вероятностей лежат в основе всех задач и формул.

Случайный эксперимент — это действие, результат которого заранее неизвестен. Например, подбрасывание монеты, бросок игрального кубика или вытягивание карты из колоды. Каждый такой эксперимент может закончиться разными исходами.

Исход — это конкретный результат случайного эксперимента. Если бросаем кубик, возможные исходы — числа от 1 до 6. Множество всех элементарных исходов образует пространство элементарных событий.

Событие в теории вероятностей — это любое подмножество исходов. Например, событие «выпало четное число» включает исходы 2, 4 и 6. События обозначают заглавными латинскими буквами: A, B, C и т. д.

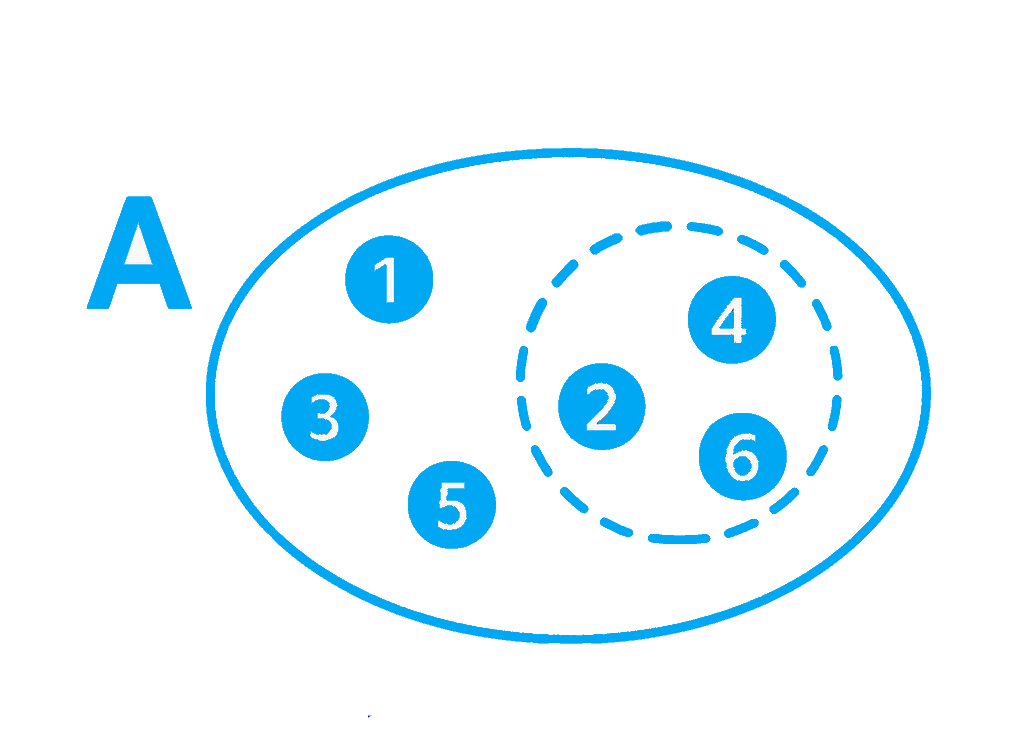
Вероятность события — это число от 0 до 1, которое показывает, насколько возможно наступление события. Если вероятность равна 0, событие невозможно. Если 1 — оно произойдет обязательно. Все значения между этими крайностями — случайные события. Например, вероятность выпадения орла при подбрасывании честной монеты — 0,5.

Пространство исходов в теории вероятности — это полный перечень всех возможных вариантов эксперимента. Например, при броске кубика — это числа от 1 до 6.

Если все исходы равновероятны, то вероятность можно рассчитать по классической формуле:

P(A) = m / n,  где:

m — число благоприятных исходов;

n — общее количество равновозможных исходов.

Например, как найти вероятность события: достать короля из колоды в 36 карт. Всего 4 короля, значит, P = 4 / 36 = 1 / 9 ≈ 0,11.

Эти понятия используют во всех формулах и рассуждениях относительно теории вероятностей, поэтому важно их запомнить и понимать на примерах.

Событие и виды событий

Событие в теории вероятностей — это результат или группа результатов случайного эксперимента, которые нас интересуют. Например, при броске кубика событием может быть «выпало четное число» или «выпала шестерка».

События делятся на несколько видов в зависимости от того, как они соотносятся друг с другом и с экспериментом:

Достоверные события обязательно произойдут. Если бросить камень, он упадет вниз — это физически гарантированный результат. Вероятность такого события всегда равна 1.

Невозможные события заведомо не произойдут. Например, у классического кубика нет цифры 8, значит, событие «выпадет 8» — невозможное. Его вероятность равна 0.

Случайные события могут произойти, а могут и нет. Если мы подбрасываем монету, выпадет орел или решка — результат нельзя предсказать заранее. Такие события встречаются чаще всего и имеют вероятность от 0 до 1.

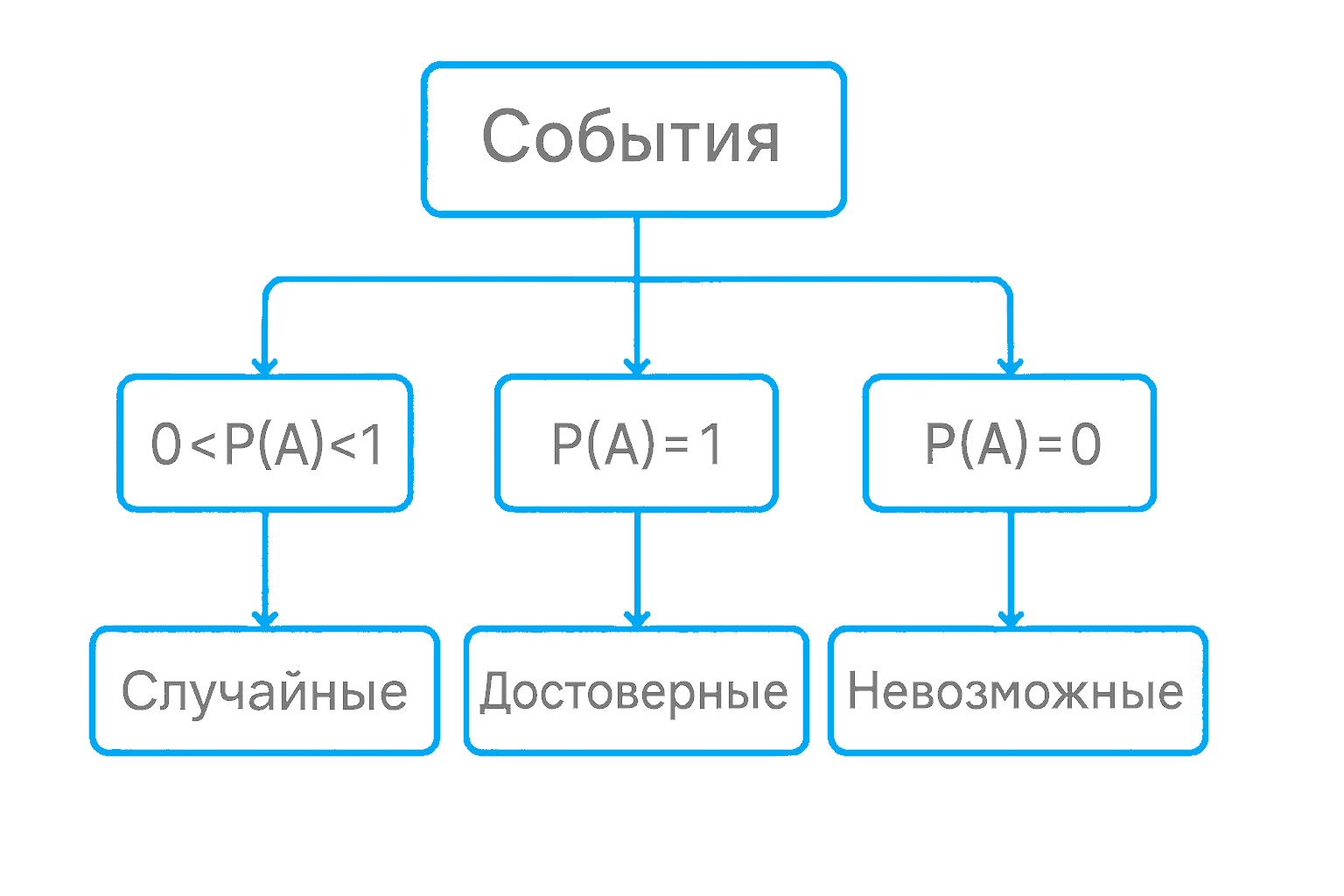
Есть и классификация по совместимости:

Несовместимые события исключают друг друга. Например, при одном броске кубика не может выпасть и двойка, и шестерка одновременно. Если происходит одно, другое исключается.

Совместимые события в теории вероятности могут происходить одновременно. Например, при броске кубика может выпасть число, которое одновременно четное и делится на 3 — это шестерка.

Также выделяют противоположные события — это пара событий, одно из которых обязательно произойдет, а другое нет. Например, если событие A — «выпала решка», то противоположное ему — «выпал орел». Это верно, если A и ¬A — противоположные (дополнительные) события, то есть события, образующие полную группу.

Иногда события образуют полную группу событий в теории вероятности — это набор несовместимых событий, среди которых обязательно произойдет одно. Например, все шесть граней игрального кубика образуют полную группу.

Понимание видов событий в теории вероятности — основа для точного расчета вероятностей в разных ситуациях.

Вероятность

Вероятность — это в математике числовая мера возможности наступления события. Она показывает, насколько велик шанс того, что произойдет нужный результат. В математике вероятность обозначается заглавной латинской буквой P, например, P(A) — обозначение вероятности события A.

Значение вероятности всегда находится в пределах от 0 до 1:

• 0 означает, что событие невозможно;
• 1 — что оно обязательно произойдет;
• любое значение между ними указывает на случайное событие с определенным шансом.

Для равновозможных исходов как посчитать вероятность события — используется формула:

P(A) = m / n, где:

m — число благоприятных исходов;

n — общее количество всех равновозможных исходов.

Например, при подбрасывании монеты благоприятный исход один — выпала решка, а общее число исходов — два (орел или решка). Тогда:

P(решка) = 1 / 2 = 0,5

Вероятность можно выразить в виде:

• дроби (1/3);
• десятичной формы (0,33);
• процентов (33%).

Также выделяют условную вероятность — когда вероятность одного события зависит от другого. Она обозначается как P(A | B).

Кроме того, важны свойства:

P(¬A) = 1 – P(A);

0 ≤ P(A) ≤ 1

Понимание, как вычислять вероятность, позволяет оценивать риски, строить прогнозы и принимать решения в условиях неопределенности.

Как найти вероятность: формулы и примеры

Чтобы рассчитать вероятность события, нужно определить общее число возможных исходов и количество исходов, которые считаются благоприятными. Если все исходы равновозможны, применяется формула нахождения вероятности:

P(A) = m / n, где:

P(A) — вероятность события A;

m — число благоприятных исходов;

n — общее количество всех исходов.

Пример 1. Как найти вероятность вытянуть из колоды 36 карт любую даму:

m = 4,

n = 36,

P = 4 / 36 = 1 / 9 ≈ 0,11, или 11%

Пример 2. Как посчитать вероятность события: при броске стандартного кубика выпадет нечетное число:

m = 3,

n = 6,

P = 3 / 6 = 0,5

Для более сложных задач:

Формула сложения вероятностей:

Если A и B — несовместные события:

P(A ∪ B) = P(A) + P(B)

Пример 3. P(2 ∪ 5) = 1/6 + 1/6 = 2/6 = 1/3 ≈ 0,33

Формула произведения вероятностей (независимые события):

P(A ∩ B) = P(A) × P(B)

Пример 4. Дважды выпала решка:

P = 0,5 × 0,5 = 0,25

Если события зависимы:

P(A ∩ B) = P(A) × P(B | A)

Пример 5. Сначала красный, потом синий шар:

P = 5/8 × 3/7 = 15/56 ≈ 0,27

Условная вероятность:

P(A | B) = P(A ∩ B) / P(B)

Пример 6. P = 0,10 / 0,20 = 0,5

Эти формулы вероятности позволяют решать задачи разной сложности. Главное — точно определить тип событий.