Формула трапеции
Содержание
ПоказатьСкрыть
Содержание
Что такое площадь трапеции?
Трапеция — это геометрическая фигура, четырехугольник с двумя параллельными сторонами, которые называются основаниями трапеции. Две другие стороны, не параллельные основаниям, являются боковыми сторонами. Площадь трапеции — это часть плоскости, заключенная внутри фигуры. В геометрии площадь обозначается как S.
Чтобы рассчитать площадь трапеции, можно использовать способ подсчета количества единичных квадратов. Для этого трапецию мысленно разделяют на небольшие квадраты со стороной 1. Считая их общее количество, можно приблизительно узнать площадь фигуры, что может быть полезно в базовых учебных задачах.
Высотой трапеции называют перпендикуляр, проведенный от одной параллельной стороны к другой. Высота — важный элемент для расчета площади трапеции, особенно если известны длины оснований.
Какие свойства у трапеции?
Трапеция обладает особым набором свойств, отличающих ее от других четырехугольников. Некоторые из них зависят от типа трапеции — равнобедренная, прямоугольная или произвольная, — однако существуют универсальные характеристики, которые подходят для любого вида:
- Свойства оснований и боковых сторон: параллельные стороны трапеции всегда называются основаниями, а две другие стороны — боковыми. Боковые стороны не равны основаниям по длине и располагаются наклонно относительно них (кроме прямоугольной трапеции).
- Свойства углов: в любой трапеции сумма углов, примыкающих к одной боковой стороне, составляет 180 градусов. Это свойство полезно для определения углов, если известны другие параметры.
- Диагонали: диагонали трапеции, как правило, не равны и пересекаются под углом, деля фигуру на два треугольника. В равнобедренной трапеции диагонали всегда равны по длине и делят друг друга пополам.
- Средняя линия: средняя линия трапеции — это отрезок, соединяющий середины боковых сторон. Ее длина равна полусумме оснований, что упрощает расчет площади, когда известна высота.
Вписанная окружность: трапеция является вписанной, если в нее можно вписать окружность. Это возможно, если сумма длин ее оснований равна сумме длин боковых сторон.
Формулы площади трапеции
Существует несколько формул для расчета площади трапеции в зависимости от доступных параметров. Рассмотрим основные способы.
Через основания и высоту
Если известны длины оснований трапеции (обозначим их a и b) и высота h, площадь можно найти по формуле: S = ½ (a+b)h.
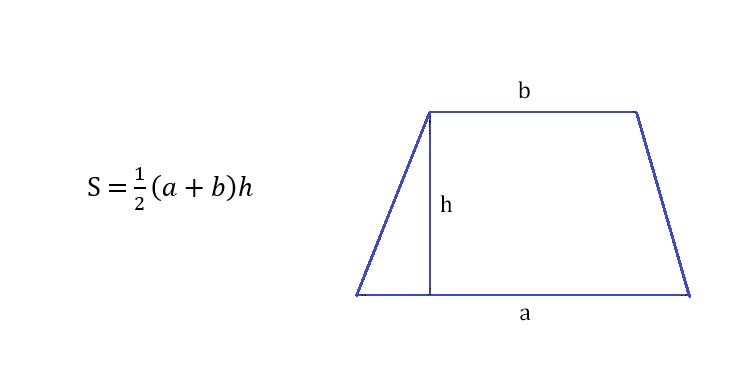
Через высоту и среднюю линию
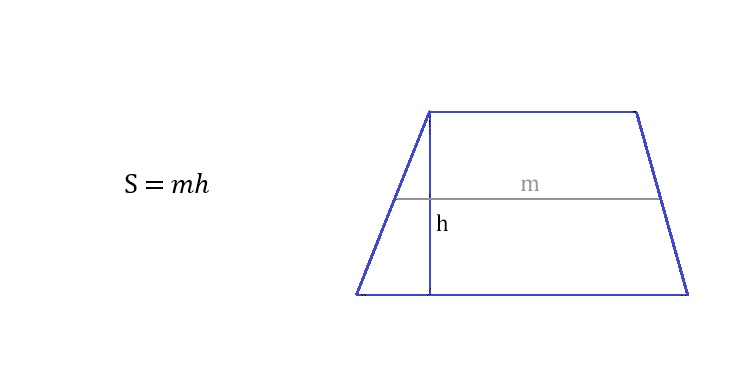
Средняя линия m трапеции определяется как полусумма оснований: m = (a + b) x 2
Зная среднюю линию и высоту, площадь трапеции можно рассчитать по формуле: S = mh
Через диагонали и угол между ними
Если известны длины диагоналей x и y, а также угол α между ними, площадь вычисляется следующим образом:
Эта формула особенно полезна для расчета площади равнобедренной трапеции.
Через четыре стороны
Когда известны длины всех сторон трапеции, площадь можно найти с помощью формулы Брахмагупты:
где p — полупериметр трапеции, который рассчитывается
По диагоналям и углу между ними
Если у фигуры диагонали x и y равны, перед нами равнобедренная трапеция. А ее площадь можно рассчитать по формуле:
Через радиус вписанной окружности и угол. Если в трапецию вписана окружность, то для вычисления площади нужно знать радиус этой окружности и угол между двумя сторонами трапеции. Необходимо сложить длины обоих оснований и умножить на половину диаметра.
Через радиус вписанной окружности и угол
Если в трапецию вписана окружность, а также известен радиус r этой окружности, площадь можно определить по формуле:
Эта формула применима только в тех случаях, когда можно вписать окружность.
Задачи на нахождение площади
Пример 1. Найдите площадь трапеции с основаниями 8 см и 12 см и высотой 5 см.
Решение:
Пример 2. Определите площадь трапеции, если средняя линия равна 6 см, а высота — 4 см.
Решение:
Пример 3. Вычислите площадь трапеции с диагоналями 10 см и 12 см, если угол между ними равен 30°.
Решение:
Пример 4. Трапеция имеет основания длиной 7 см и 10 см, радиус вписанной окружности — 3 см. Найдите ее площадь.
Решение:



