Действительные числа

Действительные числа: что это

Действительные, или, вещественные числа – это все числа, которые можно встретить в повседневной жизни. В их состав входят:

• положительные числа (например, 5, 12, 3.7);
• отрицательные числа (например, -8, -2.5, -0.3);
• ноль.

Множество действительных чисел включает в себя рациональные и иррациональные .

Обозначение множества действительных чисел – R.

С этими числами можно выполнять основные арифметические операции: сложение, вычитание, умножение и деление.

Свойства действительных чисел

Рациональные числа

Рациональные числа – те, которые можно представить в виде дроби m/n, где m и n – целые числа, а n ≠ 0 (например, 3/4, -2, 0.5).

Примеры рациональных чисел:

• 3/4;
• -2;
• 0.25 (так как 0.25 = 1/4).

Иррациональные числа

Иррациональными числами называют числа, которые нельзя записать в виде дроби. Их десятичная запись бесконечна и не содержит повторяющегося периода.

Примеры иррациональных чисел:

• π ≈ 3.141592...;
• √2 ≈ 1.414213....

Бесконечность

Действительные числа могут быть:

• конечными – это обычные числа, например, 5, -12,7, 3/4;
• бесконечными – это числа, которые не имеют конечного представления, например, π или √2.

Множество действительных чисел не ограничено, то есть можно найти числа, которые будут больше или меньше любого заданного числа.

Классификация действительных чисел

Положительные, отрицательные и ноль

Действительные числа можно разделить на три группы:

• положительные числа – больше нуля (например, 2, 3.5, 100);
• отрицательные числа – меньше нуля (например, -5, -1.2, -30);
• ноль (0) – не является ни положительным, ни отрицательным числом, но относится к множеству действительных чисел.

Целые числа

Целыми числами называют числа, которые не содержат дробной или десятичной части. Они включают:

• натуральные числа – 1, 2, 3, 4 и так далее;
• ноль (0);
• отрицательные числа – -1, -2, -3 и так далее.

Примеры целых чисел: -3, -2, -1, 0, 1, 2, 3.

Натуральные числа

Натуральные числа – это положительные целые числа, которые используются для счета предметов.

Примеры: 1, 2, 3, 4, 5, 6 и так далее.

Некоторые математические определения включают ноль в множество натуральных чисел, но чаще всего натуральные числа начинают с единицы.

Представление действительных чисел

Действительные числа можно записывать разными способами. Чаще всего используют десятичное представление, но также существуют дробное и экспоненциальное представления.

Десятичное представление

Число записывают с помощью целой и дробной части. Например:

• 2,5 – десятичное представление числа 2 с половиной.
• 3,14159265… – десятичное представление числа π, где цифры после запятой бесконечны.

Десятичное представление бывает двух видов:

• конечное – число имеет ограниченное количество знаков после запятой (например, 0,75, 2,125);
• бесконечное – число имеет бесконечную последовательность цифр после запятой (например, π = 3.14159265..., √2 = 1.41421356...).

Дробное представление

Часть действительных чисел можно записать в виде обыкновенной дроби m/n, где:

• m – числитель (целое число);
• n – знаменатель (целое число, не равное нулю).

Примеры:

• число 0,5 можно записать как дробь ½;
• число 3/4 остается в виде дроби, но его десятичное представление – 0,75;
• иррациональные числа (например, π = 3.14159265...) нельзя записать в виде дроби.

Экспоненциальное представление

Этот способ удобен для записи очень больших или очень маленьких чисел. Число представляют в виде мантиссы и порядка.

Примеры записи большого числа:

• число 1 000 000 можно записать как 10⁶ (так как 1 000 000 = 10 × 10 × 10 × 10 × 10 × 10);
• если число содержит десятичную часть, например 5 200 000, его можно записать как 5.2 × 10⁶.

Примеры записи маленького числа:

• число 0.00034 можно записать как 3.4 × 10⁻⁴ (здесь порядок -4 показывает, что запятая передвинута на 4 разряда влево).

Экспоненциальная форма записи используется в науке и вычислениях, где важны точность и компактность представления чисел.

Сравнение действительных чисел

На множестве R (действительных чисел) выполняются все основные математические законы, включая формулы сокращенного умножения. Например:

a² - b² = (a - b)(a + b)

Эта формула справедлива не только для рациональных чисел, но и для всех действительных.

Коммутативные законы:

a + b = b + a

a * b = b * a

Эти правила означают, что порядок сложения и умножения не влияет на результат.

Любые два действительных числа можно сравнивать. Число a считается больше числа b, если оно расположено правее на числовой прямой.

Для определения порядка чисел можно вычислить их разность:

Если a - b > 0, то a > b.

Если a - b < 0, то a < b.

Если a - b ≤ 0, то a ≤ b.

Примеры:

6 > 2, так как 6 - 2 = 4 > 0

-8 < -5, так как -8 - (-5) = -8 + 5 = -3 < 0

3 > 2; -3 > -5

Сравнение десятичных дробей выполняется поразрядно:

Если a₁ > b₁, то a > b.

Если a₁ = b₁, сравнивают следующий разряд.

Если числа равны до какого-то разряда, но одно из них периодическое, содержащие 9 в периоде, его можно заменить на эквивалентную запись с нулем.

Пример:

0.49999999... = 0.5

Бесконечные десятичные дроби не имеют периода, состоящего только из 9.

Действительные числа удобно представлять на числовой прямой.

Поэтому числовая прямая часто используется как визуальное представление множества действительных чисел.

Наглядно представить действительные числа можно с помощью координатной прямой.

Координатная прямая и действительные числа

Координатная прямая – это своеобразная числовая «карта», которая показывает расположение чисел относительно друг друга на горизонтальной линии.

Основные особенности координатной прямой:

• Точка отсчета. В центре координатной прямой находится ноль (0) – отправная точка. Числа справа от нуля положительные, а слева – отрицательные.
• Направление. Числа увеличиваются слева направо. Чем дальше число вправо, тем оно больше.
• Равные расстояния. Числа расположены на равных промежутках. Например, расстояние между 0 и 1 такое же, как между -1 и 0.
• Дробные и иррациональные числа. На координатной прямой можно отметить не только целые числа, но и дробные (например, 0.75, 1/2), а также иррациональные (√2, π).

Обратите внимание, координатную прямую используют только для действительных чисел. Комплексные числа на ней разместить нельзя, так как у них есть мнимая часть, требующая дополнительной оси.

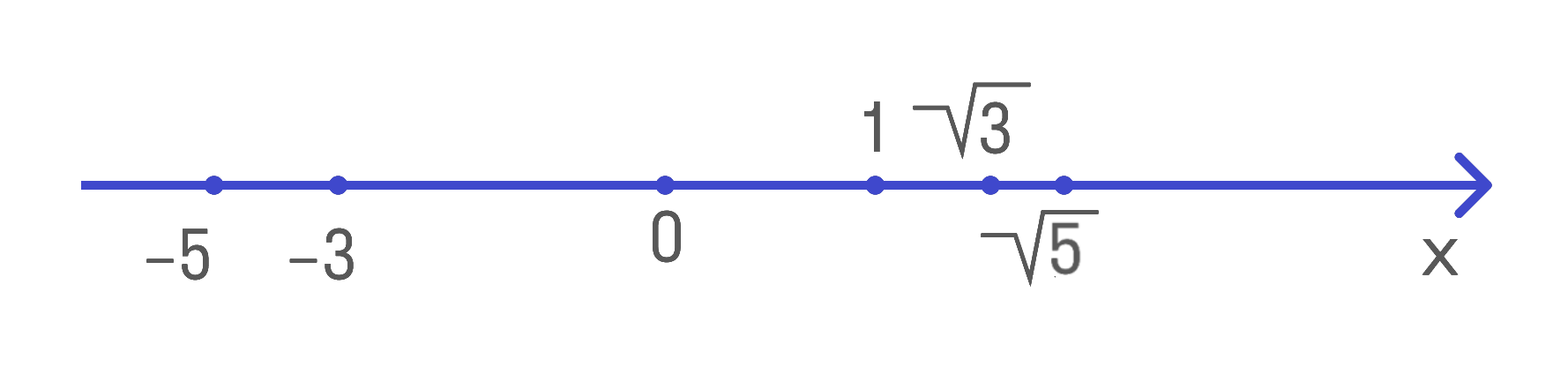
Пример расположения чисел на координатной прямой

На прямой можно отметить:

• -2, -1, 0, 1, 2 – целые числа;
• 1/2, 0.75 – дробные числа;
• √2 ≈ 1.414, π ≈ 3.141 – иррациональные числа.

Таким образом, координатная прямая – это удобный способ визуально представить множество действительных чисел и показать их взаимное расположение.

Множество действительных чисел

Множество действительных чисел обозначается буквой R. Оно объединяет в себе все известные числовые множества.

К этим множествам относятся:

Множество натуральных чисел (N) – это числа, используемые для счета предметов: 1, 2, 3, 4, …

Множество целых чисел (Z) – включает в себя натуральные числа, их отрицательные значения и ноль: ..., -3, -2, -1, 0, 1, 2, 3, …

Множество рациональных чисел (Q) – числа, которые можно представить в виде дроби m/n, где m и n – целые числа, а n ≠ 0.

• Рациональное число может быть записано как конечная десятичная дробь:
  
  0.5 = 1/2.
• Либо как бесконечная периодическая десятичная дробь:
  
  0.333... = 1/3.

Рациональные числа позволяют производить точные измерения, но иногда приходится использовать приближенные значения. Например:

Приближение для √2:

1,4 – грубое приближение;

1,41 – точнее.

Однако √2 – это не рациональное, а иррациональное число, так как его десятичное представление бесконечно и непериодично.

Множество иррациональных чисел (I) – числа, которые нельзя представить в виде дроби m/n. Их десятичная запись бесконечна и не имеет повторяющегося периода. Примеры: √2, π, e.

Множества рациональных и иррациональных чисел не пересекаются, так как число не может быть одновременно и рациональным, и иррациональным.

Если объединить множество рациональных и множество иррациональных чисел, получится множество действительных чисел (R).

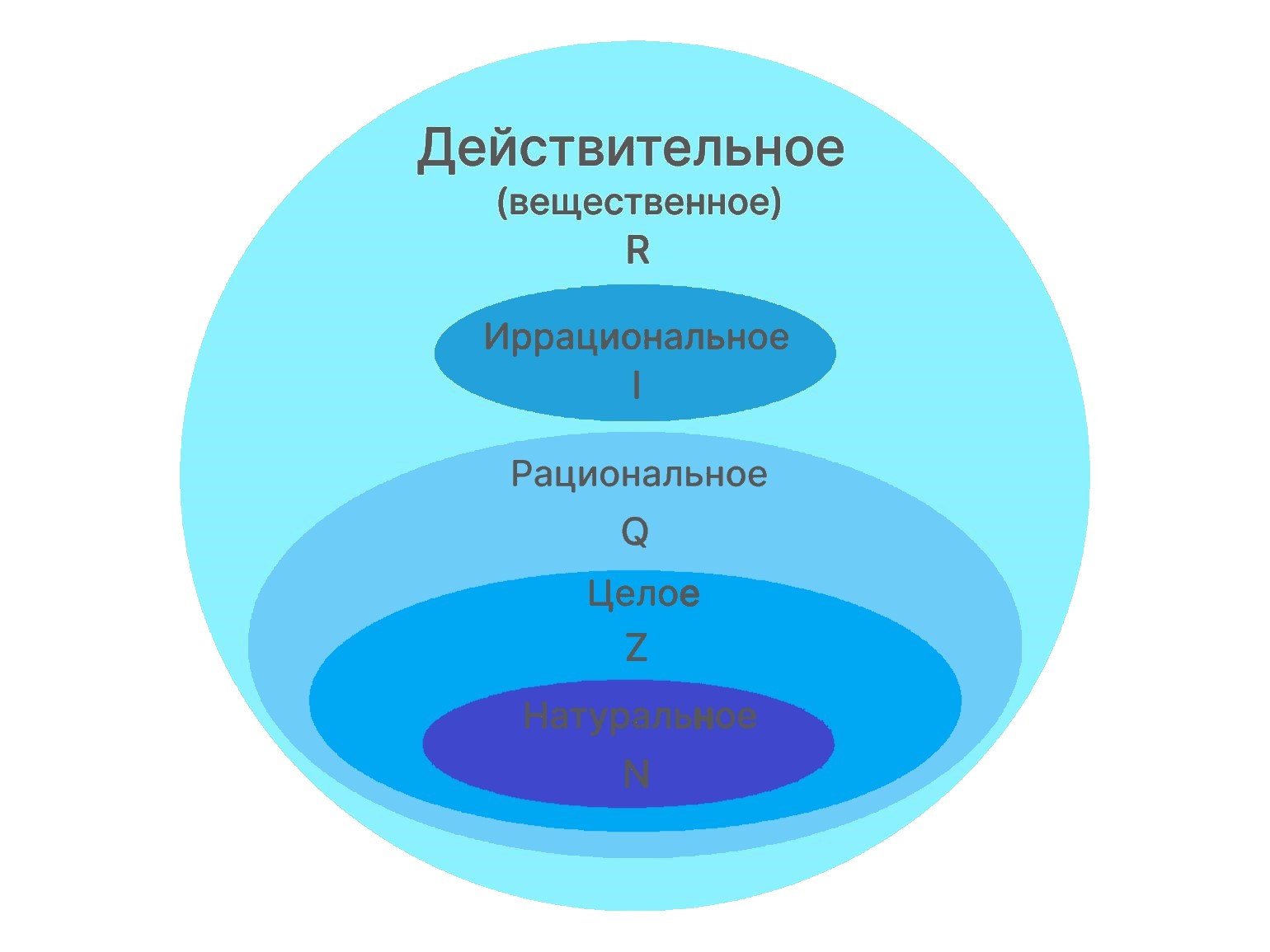
Соответствие множества действительных чисел числовой прямой

Каждому действительному числу соответствует единственная точка на числовой прямой. Координата этой точки может быть как рациональной, так и иррациональной.

Это создает взаимооднозначное соответствие между множеством R и множеством всех точек координатной прямой:

• каждое число x имеет только одну точку на числовой прямой;
• каждой точке на числовой прямой соответствует единственное число x.

Поэтому числовая прямая и множество действительных чисел – это фактически одно и то же.

Формулы и законы для множества действительных чисел

На множестве R действительных чисел выполняются все стандартные математические законы:

• Формулы сокращенного умножения, например:
  
  a² - b² = (a - b)(a + b).
• Коммутативные законы:
  
  a + b = b + a;
  
  a * b = b * a.

Множество действительных чисел можно представить в виде вложенных множеств:

• N – натуральные числа: 1, 2, 3, 4, …
• Z – целые числа: ..., -3, -2, -1, 0, 1, 2, 3, …
• Q – рациональные числа: 1/2, -3, 0.333..., 2.5.
• I – иррациональные числа: √2, π, e.
• R – объединение рациональных и иррациональных чисел.

То есть:

N ⊂ Z ⊂ Q ⊂ R.

Парадокс сравнения бесконечных множеств

Рассмотрим множество натуральных чисел N:

N = {1, 2, 3, 4, 5, ...}.

Множество четных чисел E:

E = {2, 4, 6, 8, ...}.

Множество чисел, кратных 10:

D = {10, 20, 30, 40, ...}.

Кажется, что в E элементов в два раза меньше, чем в N, а в D – еще меньше. Однако все эти множества содержат одинаковое количество элементов, так как между ними можно установить взаимооднозначное соответствие:

1 → 2, 2 → 4, 3 → 6, 4 → 8, ...

То есть, несмотря на то что E – это подмножество N, их количество элементов одинаково. Это особенность бесконечных множеств.