Длина окружности

Длина окружности — это

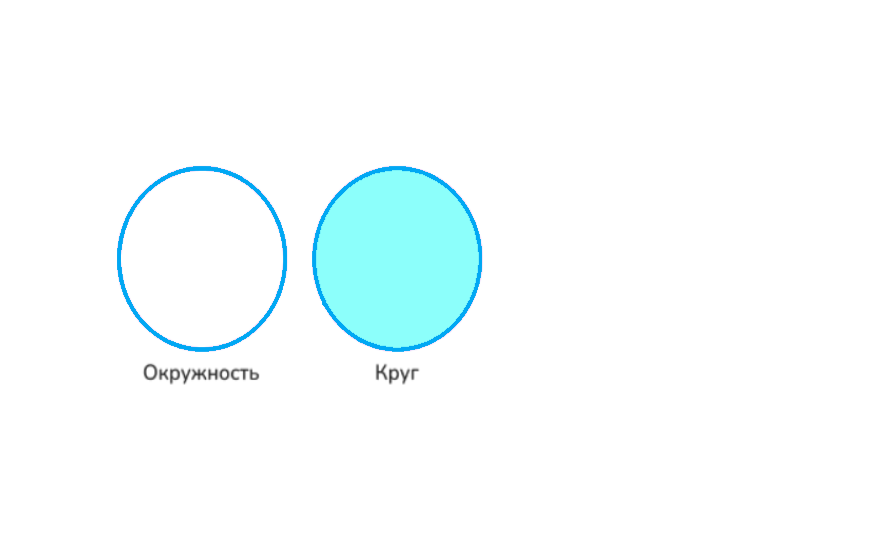
Сначала вспомним, что такое окружность и круг.

Окружность — это линия, состоящая из всех точек на плоскости, которые находятся на одинаковом расстоянии от центра. Это расстояние называется радиусом. Если выбрать точку и задать определенный радиус, получится окружность.

Дополнительно разберем несколько  важных понятий:

• Хорда — это отрезок, соединяющий две любые точки окружности.
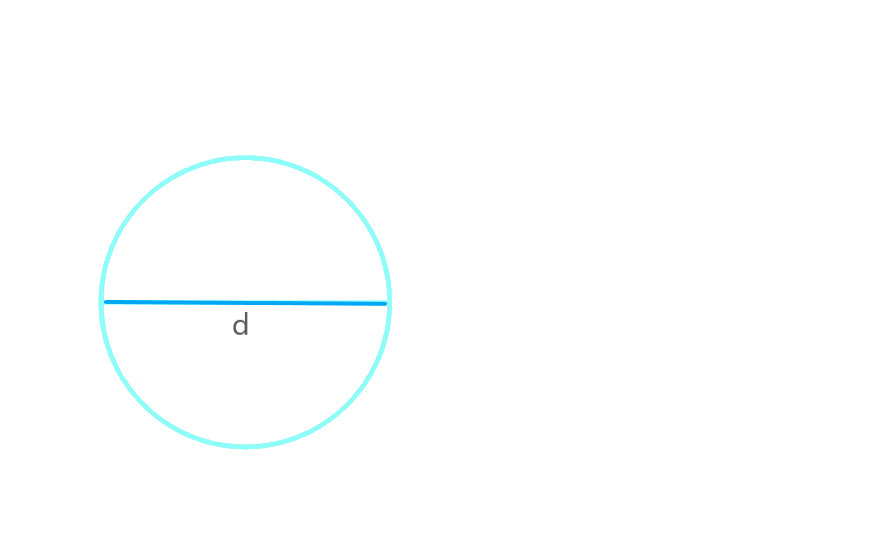
• Диаметр — это особый вид хорды, который проходит через центр окружности. Диаметр всегда в два раза больше радиуса.
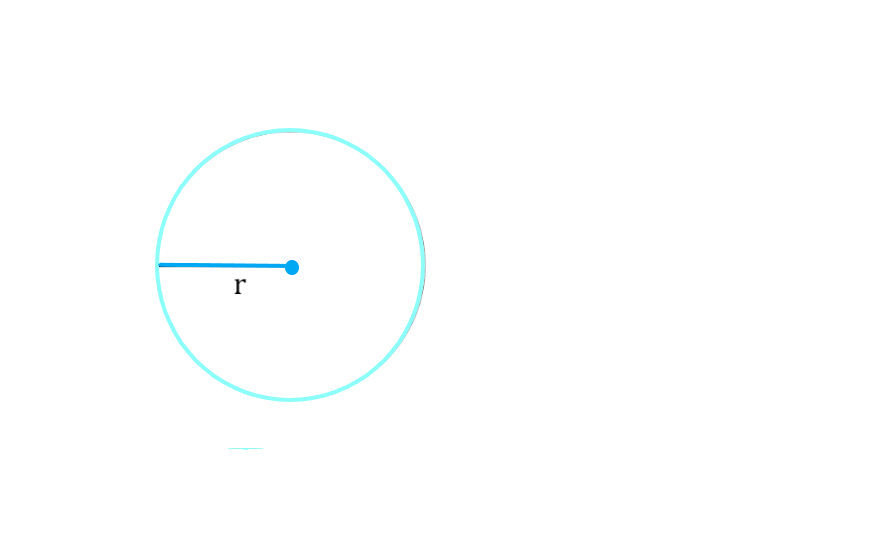
• Радиус (r) — это отрезок, соединяющий центр окружности с любой ее точкой. Например, если центр обозначен как O, а точка на окружности — как A, то OA = r.

Круг — это вся область внутри окружности вместе с самой окружностью.

Если взять окружность и развернуть ее в линию, получится ее длина. Так, длина окружности (L или С) — это длина линии, которая ограничивает круг. Ученые давно заметили, что длина окружности зависит от ее диаметра. Чем больше диаметр, тем длиннее окружность.

Формула длины окружности

Математики выяснили, что отношение длины окружности к ее диаметру всегда одинаково. Это число называется π (пи). Оно примерно равно 3,14, но на самом деле представляет собой бесконечную непериодическую десятичную дробь.

Формула длины окружности:

C=πd,

где C — длина окружности, d — диаметр, π ≈ 3,14.

Так как диаметр — это два радиуса (d = 2r), формулу можно записать иначе:

C=2πr,

где r — радиус окружности.

Если окружность поделить на части, можно измерить длину отдельной дуги.

• Если центральный угол дуги α измеряется в градусах, ее длина вычисляется так: L=παr / 180
• Если угол α измеряется в радианах, формула проще: L=αr

Число π используется в математике, физике и даже в компьютерных вычислениях. Сегодня его значение рассчитано с точностью до триллионов знаков после запятой.

Интересные факты о длине окружности

• Древняя загадка. Люди пытались измерять длину окружности с давних времен, но долгое время точность оставалась ограниченной. В III веке до н. э. древнегреческий ученый Архимед вывел формулу, которой мы пользуемся до сих пор.
• Число π — основа расчетов. Во всех формулах длины окружности присутствует π — математическая константа, приблизительно равная 3,14.
• Обозначения длины окружности. Чаще всего ее обозначают буквой C, но иногда встречается вариант L.

Как найти длину окружности

Длину окружности можно найти с помощью одной из двух формул, в зависимости от того, какие данные в задаче.

Если известен радиус (R)

C=2πR,

где:

• C — длина окружности;
• π ≈ 3,14;
• R — радиус круга.

Формула длина окружности через диаметр (D)

C=πD,

где:

• C — длина окружности;
• π ≈ 3,14;
• D — диаметр круга.

Так как диаметр — это два радиуса (D = 2R), формулы взаимосвязаны:

C=πD=2πR.

Выбор формулы зависит от того, что дано в задаче: радиус или диаметр.

Если известна площадь круга

Если известна площадь круга (S), то для нахождения длины окружности потребуется выполнить несколько шагов.

1. Вспоминаем формулу площади круга:

S=πr2,

где:

• S — площадь круга;
• r — радиус круга;
• π ≈ 3,14.

2. Выражаем радиус через площадь:

r = √S / π.

3. Подставляем найденный радиус в формулу длины окружности:

C=2πr.

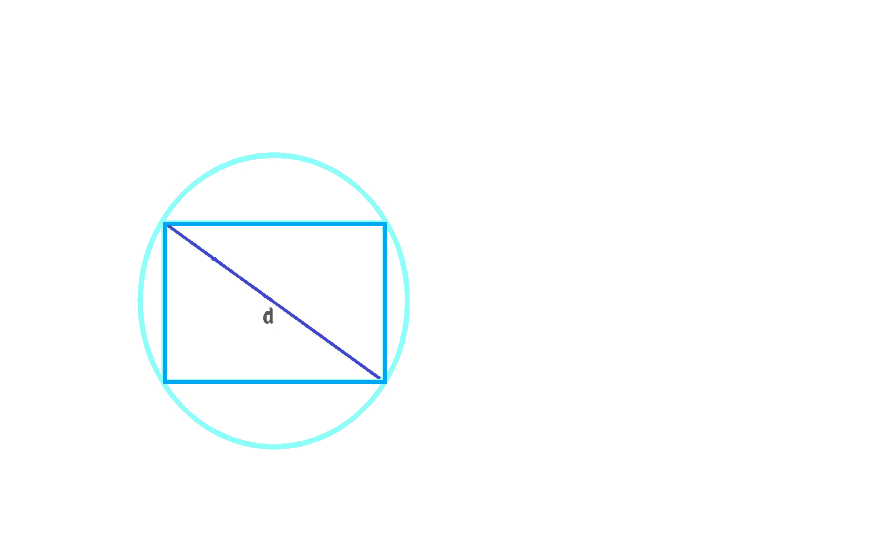
Через диагональ вписанного прямоугольника

Если в окружность вписан прямоугольник, то его диагональ (d) совпадает с диаметром окружности. Это позволяет вычислить длину окружности по формуле:

C=πd,

где:

• C — длина окружности;
• d — диагональ вписанного прямоугольника (она же диаметр окружности);
• π ≈ 3,14.

Через сторону описанного квадрата

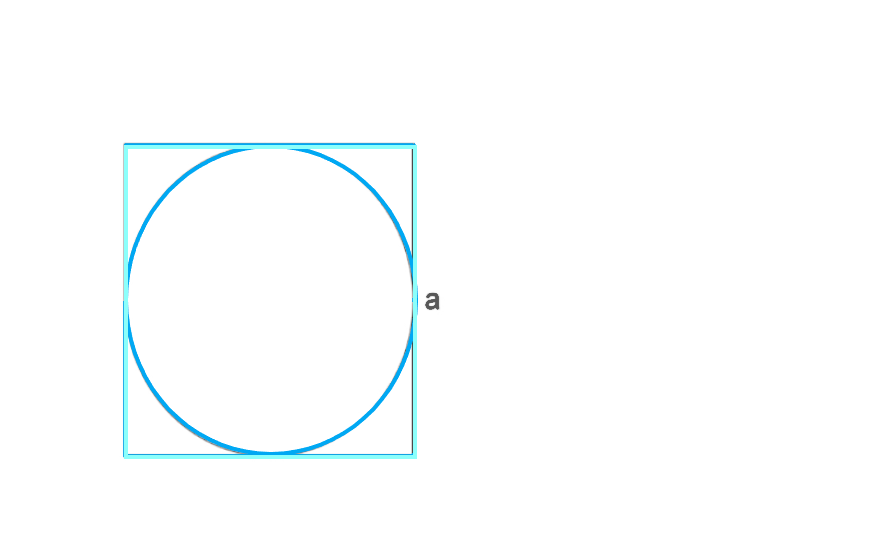
Если окружность вписана в квадрат, то ее диаметр равен длине стороны квадрата (a). Это позволяет вычислить длину окружности по формуле:

C=πa

где:

• C — длина окружности;
• a — длина стороны квадрата (она же диаметр окружности);
• π ≈ 3,14.

Примеры нахождения длины окружности

Пример 1: Найдем длину окружности по радиусу

Условие: Велосипедное колесо имеет радиус 35 см. Найдите длину окружности колеса.

Решение:

Используем формулу:

C=2πr.

Подставляем значения:

C=2×3,14×35=219,8 см.

Ответ: Длина окружности колеса 219,8 см.

Пример 2: Найдем длину окружности по диаметру

Условие: Окружность имеет диаметр 1,5 м. Чему равна ее длина?

Решение:

Формула для нахождения длины окружности через диаметр:

C=πd.

Подставляем значения:

C=3,14×1,5=4,71 м.

Ответ: Длина окружности 4,71 м.

Пример 3: Найдем длину окружности через сторону вписанного квадрата

Условие: В окружность вписан квадрат со стороной 12 см. Найдите длину окружности.

Решение:

Сторона квадрата — это диаметр окружности, значит, используем формулу:

C=πd=πa.

Подставляем значения:

C=3,14×12=37,68 см.

Ответ: Длина окружности 37,68 см.