Формулы приведения
Содержание
ПоказатьСкрыть
Содержание
Формулы приведения в тригонометрии
Формулы приведения — это выражения, которые позволяют упростить тригонометрические функции углов вида πn/2 + α, где n — целое число от 1 до 4, а α — угол в пределах от 0 до π/2. Они помогают преобразовать функцию так, чтобы аргумент стал удобным для вычислений.
Основные факты о формулах приведения
- Формулы делятся на 4 группы в зависимости от базового угла: π/2, π, 3π/2, 2π.
- Всего существует 32 формулы, но их можно вывести по единому правилу.
- Для доказательства формул достаточно знать всего 4 выражения — это формулы сложения и разности для синуса и косинуса.
Правило приведения тригонометрических функций
Чтобы привести тригонометрическую функцию к более удобному виду, нужно определить знак и проверить, меняется ли название функции.
Сначала определяется знак: он остается таким же, как у исходного выражения, если считать, что угол α находится в первой четверти.
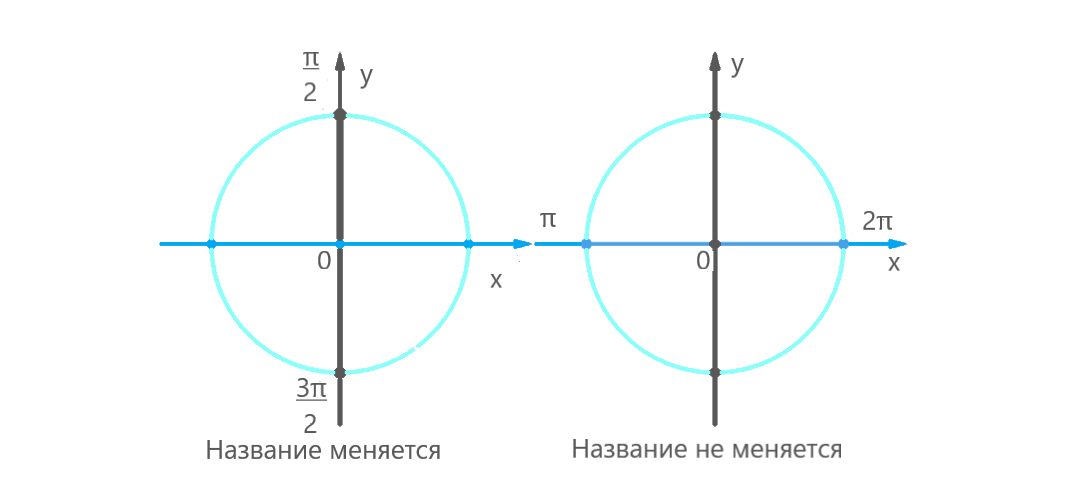
Далее проверяется, меняется ли название функции. Это зависит от того, от какой оси откладывается угол:
- если угол отсчитывается от вертикальной оси (π/2 ± α или 3π/2 ± α), название функции меняется. Синус превращается в косинус, косинус — в синус, тангенс — в котангенс, котангенс — в тангенс;
- если угол отсчитывается от горизонтальной оси (π ± α или 2π ± α), название остается тем же.
Формулы приведения помогают упростить тригонометрические функции, если их аргумент выходит за пределы от 0° до 90° (или от 0 до π/2 в радианах). Они позволяют заменить функции с «большими» углами на эквивалентные выражения с меньшими аргументами.
Но как это работает? Давайте разберемся.
Что такое опорная точка и почему она важна
Чтобы понять, как работают формулы приведения, представьте тригонометрическую окружность. Любой угол можно отложить на ней, но его положение будет зависеть от того, в каком квадранте он находится.
Например, угол 150° (или 5π/6 в радианах) расположен во втором квадранте, а 270° (3π/2) — на границе между третьим и четвертым. Вместо того чтобы запоминать значения тригонометрических функций для всех возможных углов, можно воспользоваться опорными точками — особыми углами, от которых удобно отсчитывать любые другие.
Опорная точка — это угол вида πn/2, где n — целое число. Эти точки определяют, как изменится тригонометрическая функция при переходе в другой квадрант.
Используя их, можно заменить синус на косинус, тангенс на котангенс, а также определить знак функции в данном квадранте.
Основные формулы приведения
Формулы различаются в зависимости от опорной точки:
1. Опорная точка π/2 (n = 1)
- sin(π/2 − α) = cos α
- sin(π/2 + α) = cos α
- cos(π/2 − α) = sin α
- cos(π/2 + α) = −sin α
- tg(π/2 − α) = ctg α
- tg(π/2 + α) = −ctg α
- ctg(π/2 − α) = tg α
- ctg(π/2 + α) = −tg α
2. Опорная точка π (n = 2)
- sin(π − α) = sin α
- sin(π + α) = −sin α
- cos(π − α) = −cos α
- cos(π + α) = −cos α
- tg(π − α) = −tg α
- tg(π + α) = tg α
- ctg(π − α) = −ctg α
- ctg(π + α) = ctg α
3. Опорная точка 3π/2 (n = 3)
- sin(3π/2 − α) = −cos α
- sin(3π/2 + α) = −cos α
- cos(3π/2 − α) = −sin α
- cos(3π/2 + α) = sin α
- tg(3π/2 − α) = ctg α
- tg(3π/2 + α) = −ctg α
- ctg(3π/2 − α) = tg α
- ctg(3π/2 + α) = −tg α
4. Опорная точка 2π (n = 4)
- sin(2π − α) = −sin α
- sin(2π + α) = sin α
- cos(2π − α) = cos α
- cos(2π + α) = cos α
- tg(2π − α) = −tg α
- tg(2π + α) = tg α
- ctg(2π − α) = −ctg α
- ctg(2π + α) = ctg α
Доказательства формул
Формулы приведения можно доказать с помощью стандартных тригонометрических тождеств. Например, чтобы доказать формулу sin(π/2 + α) = cos α,
используем формулу суммы синуса:
sin(α + β) = sin α ⋅ cos β + cos α ⋅ sin β.
Подставляем α = π/2:
sin(π/2 + α) = sin(π/2) ⋅ cos α + cos(π/2) ⋅ sin α
Так как sin(π/2) = 1, а cos(π/2) = 0, получаем:
sin(π/2 + α) = 1 ⋅ cos α + 0 ⋅ sin α = cos α.
Доказательство формулы cos(π + α) = −cos α.
Используем формулу суммы косинуса:
cos(α + β) = cos α ⋅ cos β − sin α ⋅ sin β.
Подставляем α = π:
cos(π + α) = cos π ⋅ cos α − sin π ⋅ sin α.
Значения cos π = −1 и sin π = 0:
cos(π + α) = (−1) ⋅ cos α − 0 ⋅ sin α = −cos α.
Такими же методами можно доказать и другие формулы.
Формулы приведения помогают упростить вычисления тригонометрических функций, приводя аргумент к диапазону от 0 до 90 градусов. Они основаны на свойствах тригонометрических функций и их значениях в опорных точках.
Теперь вы можете легко работать с тригонометрией даже при сложных углах.
Таблица формул приведения
Ниже таблица формул приведения, которая поможет легко находить эквивалентные выражения для тригонометрических функций.
Как пользоваться таблицей:
- Найдите строку с нужной тригонометрической функцией.
- Выберите столбец с соответствующим аргументом.
- На их пересечении будет упрощенный вариант функции.
Допустим, нужно упростить cos(π + α).
- Находим строку cos.
- Выбираем столбец π + α.
- На пересечении видим −cos α.
Значит, cos(π + α) = −cos α.
Таблица формул приведения
| Функция | π/2 − α | π/2 + α | π − α | π + α | 3π/2 − α | 3π/2 + α | 2π − α | 2π + α |
| sin | cos α | cos α | sin α | −sin α | −cos α | −cos α | −sin α | sin α |
| cos | sin α | −sin α | −cos α | −cos α | −sin α | sin α | cos α | cos α |
| tg | ctg α | −ctg α | −tg α | tg α | ctg α | −ctg α | −tg α | tg α |
| ctg | tg α | −tg α | −ctg α | ctg α | tg α | −tg α | −ctg α | ctg α |
Как запомнить формулы приведения
Учить все формулы приведения наизусть не обязательно. Можно воспользоваться логикой и запомнить мнемонический алгоритм, который поможет быстро находить нужное выражение.
Алгоритм запоминания:
- Представьте аргумент в удобной форме.
Любой угол можно записать в виде πn/2 ± α, где n — целое число, а α — острый угол (0 ≤ α ≤ π/2). - Нарисуйте угол на тригонометрической окружности.
Можно сделать это мысленно или на бумаге. Это поможет определить, в какой четверти находится угол. - Определите знак функции.
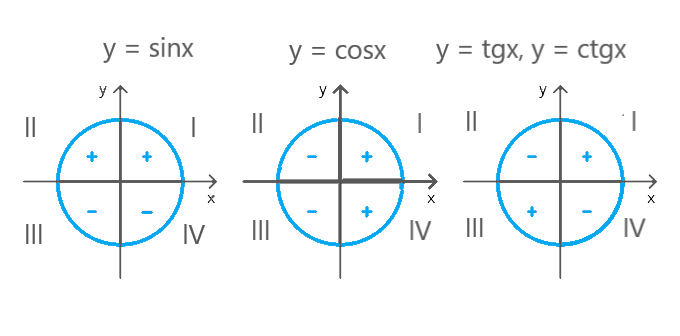
Вспомните знаки тригонометрических функций в каждой четверти:- I четверть (0 — π/2): все функции положительные;
- II четверть (π/2 — π): sin и ctg положительны, cos и tg отрицательны;
- III четверть (π — 3π/2): tg и ctg положительны, sin и cos отрицательны;
- IV четверть (3π/2 — 2π): cos и sin отрицательны, tg и ctg положительны.
- Полученная функция в правой части будет иметь тот же знак.
- Меняется ли название функции?
- Если n — нечетное (опорная точка на вертикальной оси), функция меняется:
- sin ↔ cos,
- tg ↔ ctg.
- Если n — четное (опорная точка на горизонтальной оси), функция остается той же.
- Если n — нечетное (опорная точка на вертикальной оси), функция меняется:
Как запомнить правило изменения функции?
Используйте «правило лошади»:
- Если опорная точка на вертикальной оси (π/2, 3π/2), представьте, что лошадка кивает вверх-вниз — это значит «да, меняем».
- Если опорная точка на горизонтальной оси (π, 2π), лошадка мотает влево-вправо — «нет, не меняем».
Универсальная формула приведения
Формулы приведения можно записать в общем виде:
f(πn/2 ± α) =
- ± f(α), если n четное (функция не меняется)
- ± cof(α), если n нечетное (функция меняется на кофункцию)
Где cof(α) — это «противоположная» функция (sin ↔ cos, tg ↔ ctg).
Этот алгоритм поможет быстро находить нужное выражение и решать задачи без запоминания всех 32 формул.
Пример решения выражения с формулой привидения
Найдите значение выражения:
2 cos(2π - α) + sin(π/2 + α) - tg(3π/2 - α).
Шаг 1. Применяем формулы приведения.
Рассмотрим каждое слагаемое отдельно.
cos(2π - α).
- Аргумент имеет вид 2π - α, где опорная точка — 2π, она лежит на горизонтальной оси.
- По «правилу лошадки» функция не меняется.
Косинус в четвертой четверти положительный, поэтому:
cos(2π - α) = cos α.
sin(π/2 + α).
- Аргумент имеет вид π/2 + α, где опорная точка — π/2, она лежит на вертикальной оси.
- По «правилу лошадки» синус меняется на косинус.
Вторая четверть: синус положительный, поэтому:
sin(π/2 + α) = cos α.
tg(3π/2 - α).
- Аргумент имеет вид 3π/2 - α, опорная точка — 3π/2, она лежит на вертикальной оси.
- По «правилу лошадки» тангенс меняется на котангенс.
Третья четверть: тангенс положительный, поэтому:
tg(3π/2 - α) = ctg α.
Шаг 2. Подставляем преобразованные выражения
2 cos(2π - α) + sin(π/2 + α) - tg(3π/2 - α) = 2 cos α + cos α - ctg α = 3 cos α - ctg α.
Ответ: 3 cos α - ctg α.



