Площадь квадрата

Формула площади квадрата

Квадрат называют правильным четырехугольником, потому что все его стороны равны, а углы прямые. Эта фигура кажется простой, но вычисление ее площади иногда вызывает трудности.

Квадрат можно представить как прямоугольник, у которого все стороны одинаковые. У него также могут быть две диагонали, которые соединяют противоположные вершины.

Мы разобрали несколько простых способов вычислить площадь квадрата. Каждая формула использует только одну известную величину. Эти методы легко запомнить и применять на практике.

Что такое площадь квадрата

Квадрат — это частный вид прямоугольника, но с равными сторонами, поэтому некоторые методы расчета площади у них совпадают. Формула выбирается в зависимости от того, какие параметры известны.

Площадь показывает, сколько места занимает фигура на плоскости. Проще говоря, это количество квадратных единиц, которыми можно полностью покрыть ее поверхность без зазоров и наложений.

Площадь квадрата — это часть площади, ограниченная сторонами этого квадрата. Для обозначения ее размеров используют целые числа, дроби или различные единицы измерения.

Для обозначения площади используют букву S, что происходит от латинского слова surface — «поверхность».

Площадь выражается в квадратных единицах. Наиболее распространенные:

• мм² (квадратные миллиметры);
• см² (квадратные сантиметры);
• м² (квадратные метры);
• км² (квадратные километры).

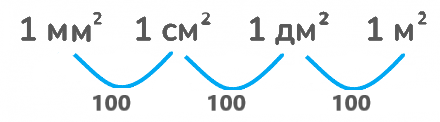
Мелкие объекты, например, стороны тетрадного листа, измеряют в квадратных сантиметрах. Для больших площадей, таких как парки или города, используют квадратные метры или километры.

Полезное о площади квадрата:

Школьники начинают изучать эту тему со 2 класса. Они учатся применять формулу площади и знакомятся с основами геометрии.

Площадь всегда выражается в квадратных единицах. В школьных задачах чаще всего встречаются мм², см², дм², м² и км². Важно приводить все значения к одной системе измерения.

Знание площади квадрата помогает вычислять площади сложных фигур. Например, разбивая многоугольник на простые элементы, можно найти их площади и сложить их для получения общего результата.

Формула площади квадрата через длину

Чтобы найти площадь квадрата, нужно умножить его сторону саму на себя, то есть возвести в квадрат.

Формула нахождения площади квадрата:

S = a × a, или, S = a²

где S — площадь, a — длина стороны квадрата.

Так как у квадрата все стороны равны, вычисление площади сводится к умножению одной стороны на себя.

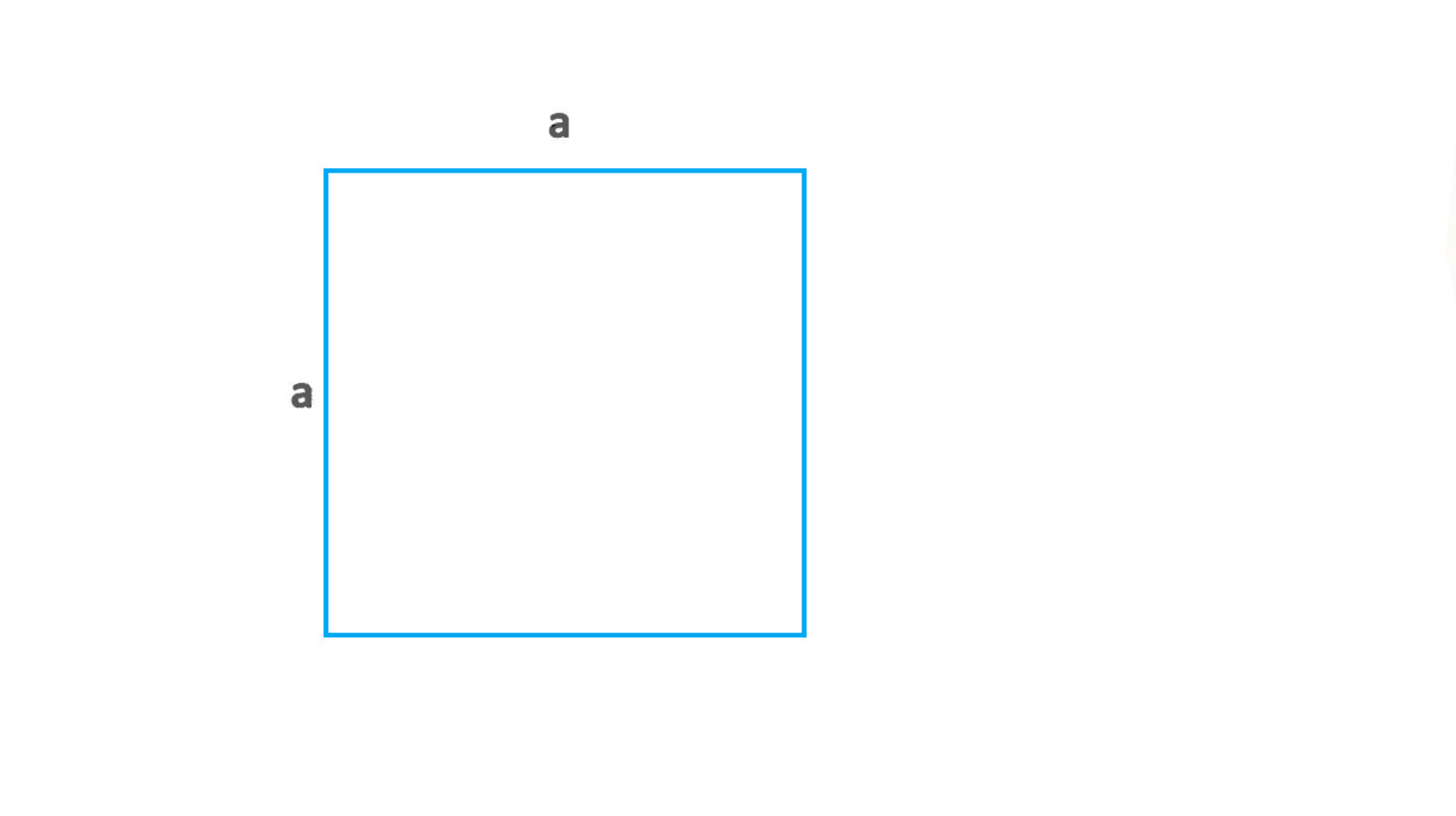
Пример расчета площади квадрата, если известна длина

Если a = 5 см, то площадь квадрата:

S = 5 × 5 = 25 см²

или

S = 5² = 25 см²

Эту формулу изучают в 3 классе. Остальные способы вычисления площади понадобятся в 8 классе.

Формула площади квадрата, если известен периметр 

Периметр квадрата — это сумма длин всех его сторон. Он рассчитывается по формуле:

P = a + a + a + a

или

P = a × 4

Если известен периметр, площадь можно найти с помощью следующей формулы:

S = P² ÷ 16

где S — площадь, P — периметр.

Пример расчета: как узнать площадь квадрата через периметр

Если P = 12 см, то:

S = 12² ÷ 16 = 144 ÷ 16 = 9 см²

Важно! Все величины должны быть в одной системе измерения. Например, если длина дана в дециметрах, а ширина в сантиметрах, их нужно привести к одной единице.

Неверный расчет:

Если длина = 2 дм, а ширина = 13 см, нельзя просто умножить 2 × 13.

Правильный расчет:

1 дм = 10 см, значит 2 дм = 20 см. Теперь можно умножать:

S = 20 × 13 = 260 см²

Чтобы избежать ошибок, всегда переводите все значения в одну систему измерения перед вычислениями.

Формула площади квадрата, если известна диагональ 

Диагональ квадрата — это отрезок, соединяющий противоположные вершины. Если известна длина диагонали, площадь можно вычислить по формуле:

S = d² ÷ 2

где S — площадь, d — диагональ.

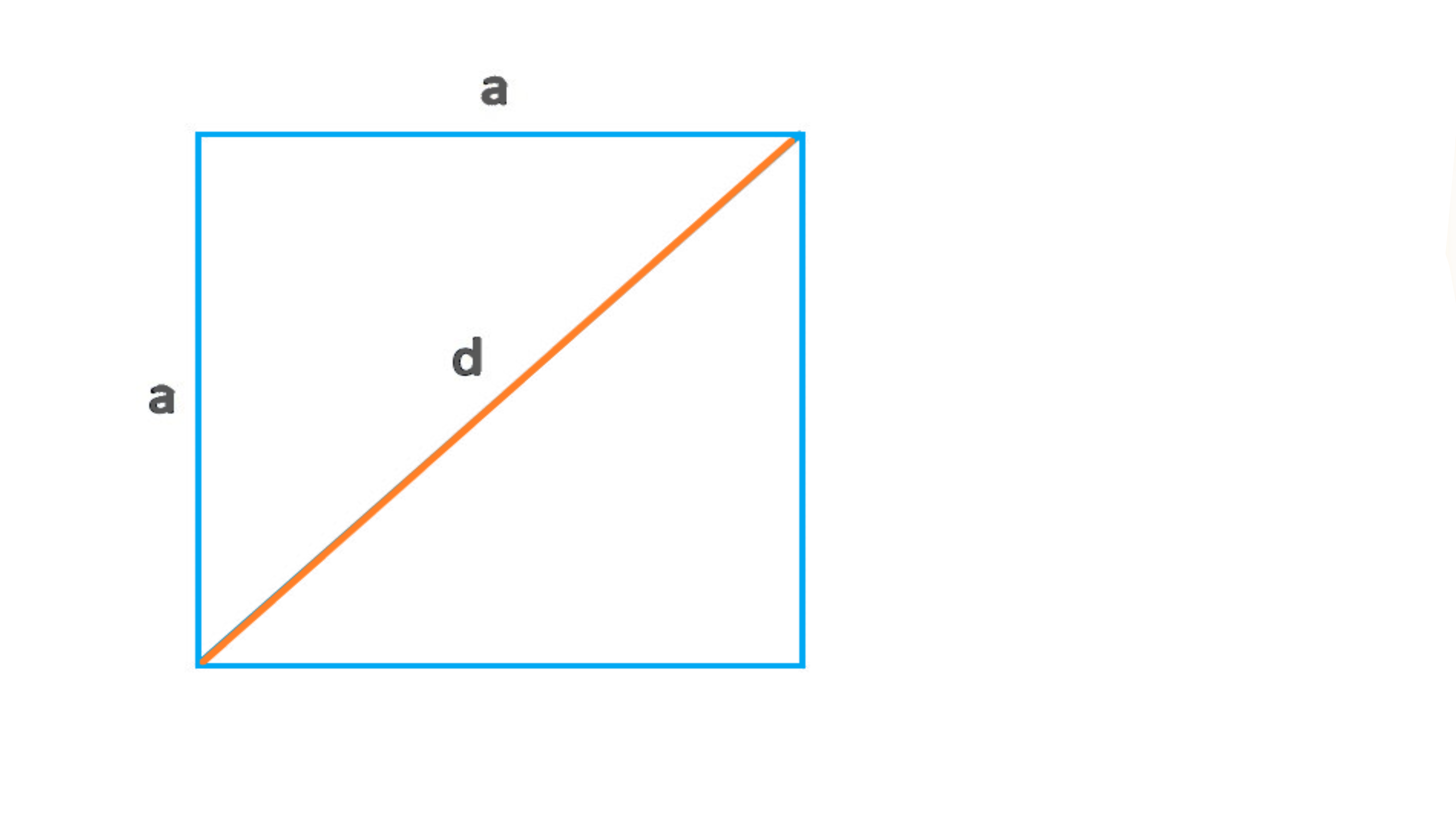
Пример расчета: как вычислить площадь квадрата через диагональ 

Если d = 10 см, то:

S = 10² ÷ 2 = 100 ÷ 2 = 50 см²

Таким образом, чтобы найти площадь через диагональ, нужно возвести ее в квадрат и разделить на два.

Формула площади квадрата через радиус окружности

Если известен радиус вписанной окружности 

Окружность считается вписанной в квадрат, если касается всех его сторон в одной точке. Радиус вписанной окружности — это расстояние от ее центра до любой точки на окружности.

Радиус вписанной окружности равен половине стороны квадрата. Чтобы найти площадь квадрата, нужно возвести этот радиус в квадрат и умножить на 4:

S = r² × 4

где S — площадь, r — радиус вписанной окружности.

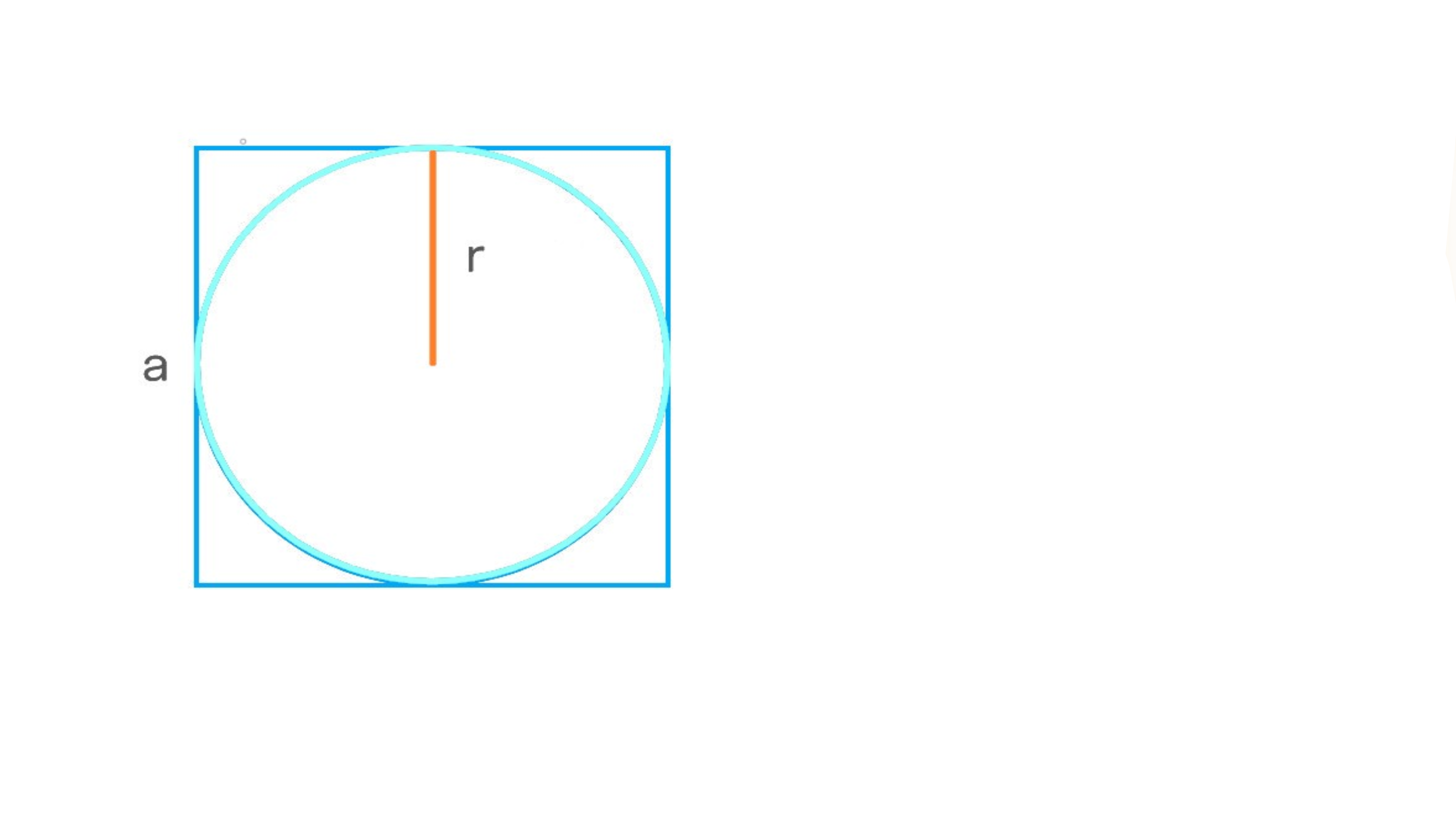
Пример расчета: как определить площадь квадрата, если известен радиус вписанной окружности

Если r = 6 см, то:

S = 6² × 4 = 36 × 4 = 144 см²

Таким образом, чтобы вычислить площадь через радиус вписанной окружности, достаточно умножить квадрат радиуса на 4.

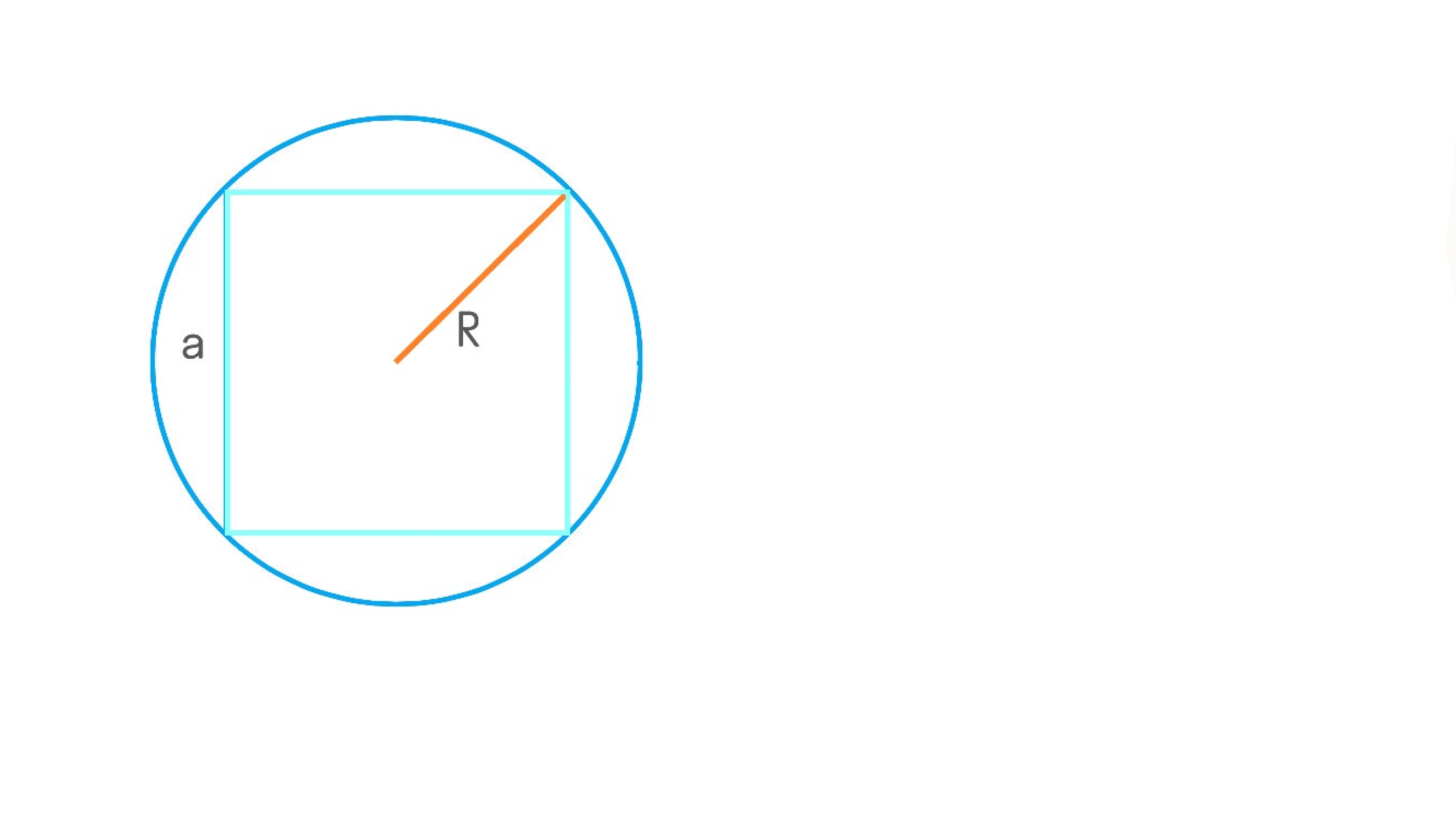
Если известен радиус описанной окружности

Окружность называется описанной, если проходит через все вершины квадрата. Радиус такой окружности обозначается заглавной буквой R.

Чтобы найти площадь квадрата через радиус описанной окружности, нужно возвести его в квадрат и умножить на 2:

S = R² × 2

где S — площадь, R — радиус описанной окружности.

Пример расчета: как найти площадь квадрата, если известен радиус описанной окружности

Если R = 10 см, то:

S = 10² × 2 = 100 × 2 = 200 см²

Таким образом, для вычисления площади через радиус описанной окружности нужно умножить его квадрат на два.

Решение задач на нахождение площади квадрата

Мы разобрали пять способов вычисления площади квадрата. Теперь попробуем применить их на практике.

Задача 1. Найдите площадь квадрата, если его диагональ равна 50 мм.

Решение:

Используем формулу:

S = d² ÷ 2

Подставляем значение диагонали:

S = 50² ÷ 2 = 2500 ÷ 2 = 1250 мм²

Ответ: 1250 мм².

Задача 2. Найдите площадь квадрата, если в него вписана окружность радиусом 10 см.

Решение:

Сторона квадрата равна диаметру окружности:

a = 2r

Используем формулу:

S = (2r)²

S = 4r²

Подставляем значение радиуса:

S = 4 × 10² = 4 × 100 = 400 см²

Ответ: 400 см².

Задача 3. Найдите площадь квадрата, если вокруг него описана окружность радиусом 14 см.

Решение:

Используем формулу:

S = R² × 2

Подставляем значение радиуса:

S = 14² × 2 = 196 × 2 = 392 см²

Ответ: 392 см².

Задача 4. Найдите площадь квадрата, если его периметр равен 24 м.

Решение:

Периметр квадрата находится по формуле:

P = 4a

Находим сторону:

a = P ÷ 4 = 24 ÷ 4 = 6 м

Теперь используем формулу площади:

S = a²

S = 6² = 36 м²

Ответ: 36 м².

Задача 5. Найдите площадь квадрата, если его сторона равна 7 см.

Решение:

Используем основную формулу площади квадрата:

S = a²

S = 7² = 49 см²

Ответ: 49 см².