Площадь ромба

Площадь ромба — это

Ромб — это четырехугольник, у которого равны все стороны. Его диагонали пересекаются под прямым углом и делят углы пополам.

Площадь ромба — это количество квадратных единиц, которое помещается внутри фигуры. Например, если ромб покрыть квадратами размером 1×1 см, то их количество и будет равно площади ромба. Площадь измеряется в квадратных единицах — см², м² и т. д.

Важное о площади ромба:

Это тема из школьной программы. Рассчитывать площадь ромба школьники учатся в 8 классе. Это задание может быть в ЕГЭ и ОГЭ.

Существуют три формулы для расчета. Выбор формулы зависит от того, какие данные вам известны.

Единицы измерения. Площадь ромба выражается в квадратных единицах. Если длина сторон или диагоналей указана в разных единицах, их нужно перевести в одинаковые.

Формула площади ромба по стороне и высоте

Есть три способа вычислить площадь ромба.

Через сторону и высоту

Площадь ромба можно найти, умножив длину его стороны на высоту.

S = a * h,

где

S — площадь ромба,

a — длина стороны,

h — высота ромба.

Через сторону и угол

Если известна длина стороны ромба и острый угол между его сторонами, площадь вычисляется так:

S = a² * sin(α),

где

S — площадь ромба,

a — длина стороны,

α — острый угол между сторонами.

Пример решения

Найдите площадь ромба, если его высота равна 6 см, а острый угол равен 30°.

Площадь ромба можно найти по формуле:

S = a * h,

где a — длина стороны ромба, h — высота.

Дана высота h = 6 и угол α = 30°. Связь высоты и стороны ромба выражается формулой:

h = a * sin(α).

Выразим сторону a:

a = h / sin(α).

Подставим значения:

a = 6 / sin(30°) = 6 / 0,5 = 12 см.

Теперь найдем площадь:

S = a * h = 12 * 6 = 72 см².

Ответ: 72 см².

Через диагонали

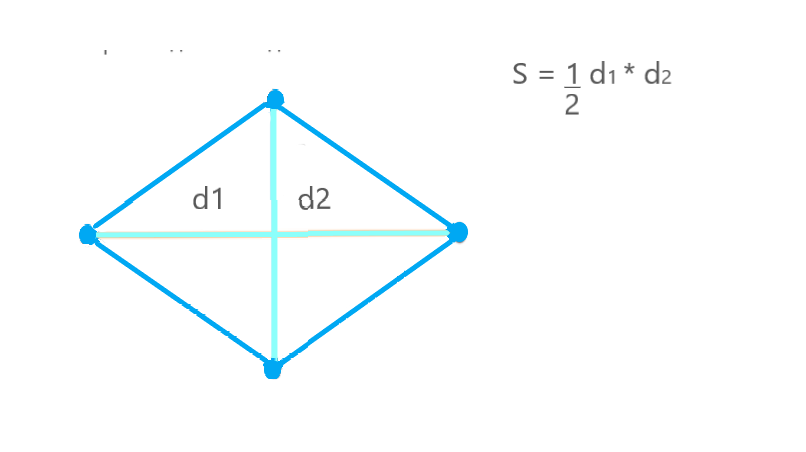
Если известны длины диагоналей ромба, его площадь можно найти через произведение диагоналей, поделенное на 2.

S = (d₁ * d₂) / 2,

где

S — площадь ромба,

d₁ — длина первой диагонали,

d₂ — длина второй диагонали.

Также формулу можно записать так:

S = 1/2 * d₁ * d₂.

Пример решения

Найдите площадь ромба, если его угол равен 60°, а периметр равен 24 см

.

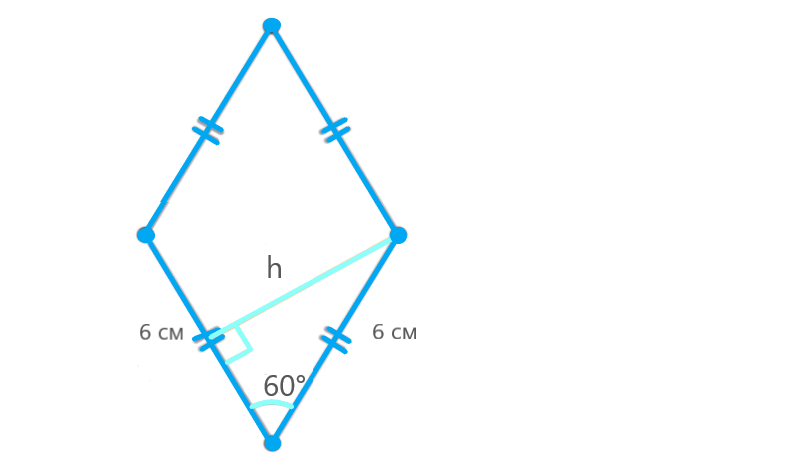
По определению ромба все его стороны равны. Если периметр равен 24 см, то длина одной стороны:

a = 24 / 4 = 6 см.

Теперь найдем высоту ромба. В ромбе высота h может быть вычислена по формуле:

h = a * sin(α),

где α = 60°. Подставим значения:

h = 6 * sin(60°) = 6 * √3 / 2 = 3√3 см.

Теперь найдем площадь ромба по формуле S = a * h:

S = 6 * 3√3 = 18√3 см².

Ответ: 18√3 см².

Площадь ромба через его диагонали

Площадь ромба составляет половину произведения его диагоналей. 

Доказательство

Воспользуемся общей формулой нахождения площади параллелограмма через его диагонали:

S = (1/2) * d₁ * d₂ * sin(α),

где d₁ и d₂ — длины диагоналей, а α — угол между ними.

В ромбе диагонали пересекаются под прямым углом, то есть α = 90°. Так как sin(90°) = 1, формула упрощается:

Таким образом, площадь ромба равна половине произведения его диагоналей.

Что и требовалось доказать.

Пример решения

Найдите площадь ромба, если его диагонали относятся как 3:4, а периметр равен 40 см.

По определению ромба все его стороны равны. Если периметр равен 40 см, то длина одной стороны:

a = 40 / 4 = 10 см.

Диагонали ромба делятся пополам и пересекаются под прямым углом. Пусть их длины равны 3x и 4x, тогда половины диагоналей равны 3x / 2 и 4x / 2.

Эти половины являются катетами прямоугольного треугольника, где гипотенуза равна стороне ромба. По теореме Пифагора:

(3x / 2)² + (4x / 2)² = 10².

Подсчитаем:

9x² / 4 + 16x² / 4 = 100,

25x² / 4 = 100,

25x² = 400,

x² = 16,

x = 4.

Длины диагоналей:

d₁ = 3x = 12 см,

d₂ = 4x = 16 см.

Теперь найдем площадь ромба по формуле:

S = 1/2 ⋅ d₁ ⋅ d₂ = 1/2 ⋅ 12 ⋅ 16 = 96 см².

Ответ: 96 см².

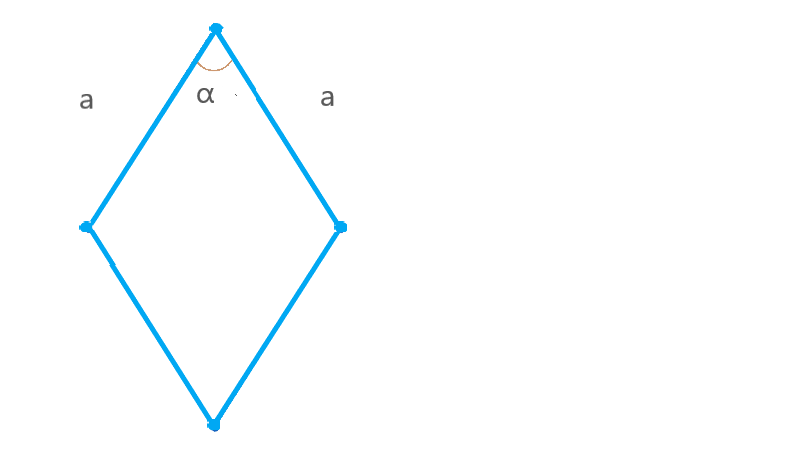
Формула площади ромба через две стороны и угол между ними

S = a² ⋅ sin(α),

где

a — сторона ромба;

α — любой угол ромба.

Пример решения

Найти площадь ромба, если каждая из его сторон равна 8 см, а угол между двумя смежными сторонами равен 45°.

Решение

Известно:

a = 8 см,

α = 45°.

Используем формулу:

S = a² ⋅ sin(α).

Подставляем значения:

S = 8² ⋅ sin(45°) = 64 ⋅ √2 / 2 = 32√2 см².

Ответ: 32√2 см².

Формула площади по радиусу вписанной окружности и углу

Формула площади ромба по радиусу вписанной окружности и углу:

S = 4 ⋅ r² ⋅ sin(α),

где:

r — радиус вписанной окружности в ромб;

α — любой угол ромба.

Пример решения

Найдите площадь ромба, если радиус вписанной окружности равен 5 см, а угол между сторонами равен 45°.

Известно:

r = 5 см

α = 45°

Формула:

S = 4 ⋅ r² ⋅ sin(α).

Подставляем значения:

S = 4 ⋅ 5² ⋅ sin(45°) = 4 ⋅ 25 ⋅ √2 / 2 = 100 ⋅ √2 / 2 = 50√2 см².

Ответ: 50√2 см².

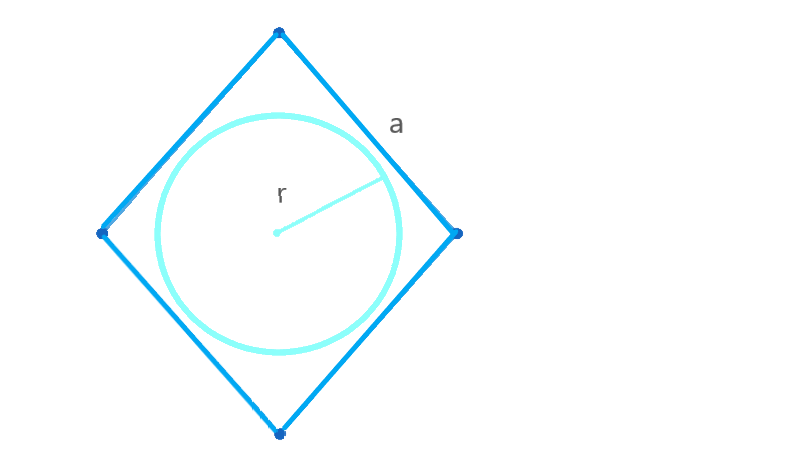
Площадь ромба по радиусу вписанной окружности и стороне

Формула площади ромба по радиусу вписанной окружности и стороне:

S = 2 ⋅ a ⋅ r,

где:

a — сторона ромба;

r — радиус вписанной окружности в ромб.

Пример решения

Найдите площадь ромба, если сторона ромба равна 6 см, а радиус вписанной окружности равен 3 см.

Известно:

a = 6 см

r = 3 см

Формула:

S = 2 ⋅ a ⋅ r.

Подставляем значения:

S = 2 ⋅ 6 ⋅ 3 = 36 см².

Ответ: 36 см².