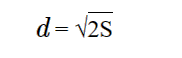Диагональ квадрата
Содержание
ПоказатьСкрыть
Содержание
Что такое диагональ квадрата?
Диагональ квадрата — это прямой отрезок, который соединяет противоположные углы фигуры и проходит через ее центр. Она равна другой диагонали, делится точкой пересечения пополам, является биссектрисой углов квадрата и образует два равных прямоугольных треугольника. Кроме того, диагонали квадрата взаимно перпендикулярны.
Чтобы вычислить диагональ квадрата, используйте формулу: d = X√2, где X — длина его стороны. Если даны дополнительные условия, например, проведенные линии под углом, их можно использовать для нахождения X, после чего подставить в формулу для определения диагонали.
Квадрат — это геометрическая фигура с четырьмя равными сторонами и четырьмя прямыми углами. Каждая сторона квадрата параллельна и равна противоположной, все углы прямые — 90°, — а диагонали равны и перпендикулярны друг другу.
В различных задачах может потребоваться найти диагональ квадрата по известному значению другой величины, такой как периметр или площадь. В таких случаях необходимо вначале использовать соответствующие формулы для вычисления длины стороны квадрата, а затем для определения его диагонали.
Диагональ любого квадрата всегда больше его стороны в два раза. По факту диагональ квадрата это квадратный корень от удвоенной суммы его стороны.
Свойства диагонали квадрата
- Обе имеют одинаковую длину.
- Делит квадрат на два равных треугольника.
- Является гипотенузой прямоугольного треугольника, образованного двумя его сторонами. Остальные две стороны треугольника являются катетами, которые также являются сторонами квадрата.
- Самый длинный отрезок внутри квадрата.
- Делит угол квадрата пополам.
- Диагонали квадрата пересекаются в его центре и образуют прямые углы.
- Она также является диаметром вписанной окружности.
- Делит квадрат на две равные площади. Каждая из получившихся половин имеет площадь, равную половине общей площади квадрата.
Как вычислить диагональ?
По периметру квадрата
Формула диагонали квадрата через периметр квадрата: d = P / 2√2
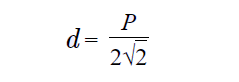
По стороне квадрата
Если известна длина стороны квадрата, то можно использовать теорему Пифагора для вычисления длины диагонали, так как диагональ делит квадрат на два равных прямоугольных треугольника и является для них гипотенузой.
Теорема Пифагора утверждает, что в прямоугольном треугольнике квадрат длины гипотенузы (c) равен сумме квадратов длин катетов (a и b). Формально она выражается так: c² = a² + b²,
где
с — гипотенуза,
a — катет,
b — катет.
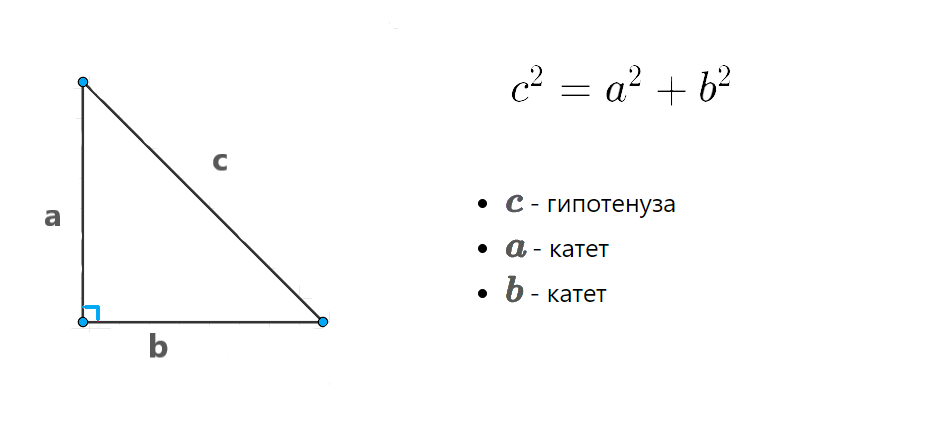
Формула для вычисления диагонали квадрата будет иметь следующий вид: d = a × √2
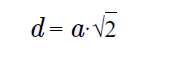
По площади квадрата
Формула диагонали квадрата через площадь квадрата: d = √2S