Формула площади параллелограмма

Площадь параллелограмма

Параллелограмм — это четырехугольник, у которого противоположные стороны параллельны. Его площадь — пространство внутри границ фигуры. Ее измеряют в квадратных миллиметрах, сантиметрах, метрах, дециметрах, километрах, гектарах и акрах.

Площадь параллелограмма можно найти разными способами в зависимости от известных параметров. О том, как найти площадь параллелограмма, расскажем ниже.

Полезное о площади параллелограмма

Древнегреческий математик Евклид в книге «Начала» дал определение площади параллелограмма и способы вычисления.

Если многоугольник состоит из нескольких других многоугольников, то его площадь равна сумме их площадей. Это правило применимо и к параллелограмму, который можно разделить, например, на два треугольника или на треугольник и трапецию.

Для вычисления площади можно использовать формулу Герона, так как диагональ делит параллелограмм на два равных треугольника:

S = 2√(p × (p - a) × (p - b) × (p - d)),

где:

a и b — смежные стороны;

d — диагональ;

p — полупериметр, который рассчитывается так:

p = P ÷ 2, где P = a + b + d.

Основные свойства параллелограмма

Свойства параллелограмма изучают в 8-м классе на уроках геометрии. Параллелограмм обладает следующими свойствами:

1. Противоположные углы равны:
   
   ∠A = ∠C, ∠B = ∠D.
2. Противоположные стороны равны:
   
   AD = BC, AB = DC.
3. Противоположные стороны параллельны:
   
   AD ∥ BC, AB ∥ DC.
4. Сумма всех углов параллелограмма равна 360°:
   
   ∠A + ∠B + ∠C + ∠D = 360°.
5. Сумма углов, прилегающих к одной стороне, равна 180°:
   
   ∠ABC + ∠BCD = ∠BCD + ∠CDA = ∠CDA + ∠DAB = ∠DAB + ∠ABC = 180°.

Формула площади по основанию и высоте

Площадь параллелограмма можно найти, если известны его основание и высота. Этот способ один из самых простых, так как напоминает вычисление площади треугольника, но без деления на два.

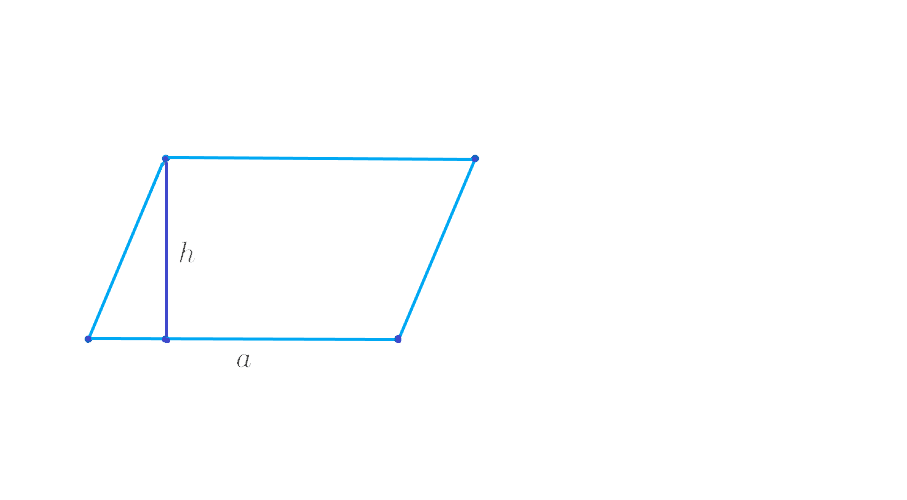
S = a × h,

где:

• a — основание;
• h — высота, опущенная на основание.

Например, найдем площадь параллелограмма, у которого основание 12 см, а высота 7 см.

Нам известно, что a = 12 см и h = 7 см.

Подставляем значения в формулу:

S = 12 × 7 = 84 см².

Ответ: площадь параллелограмма равна 84 см².

Площадь параллелограмма через стороны и угол

Площадь параллелограмма можно найти, если известны две его смежные стороны и угол между ними.

Для этого используют формулу S = a × b × sin(α),

где:

• a и b — стороны параллелограмма;
• α — угол между ними.

Например, найдем площадь параллелограмма, у которого стороны 8 см и 6 см, а угол между ними 60°.

Нам известно, что a = 8 см, b = 6 см и α = 60°.

Подставляем значения в формулу:

S = 8 × 6 × sin(60°) ≈ 8 × 6 × 0,866 ≈ 41,57 см².

Ответ: 41,57 см².

Формула площади параллелограмма через диагонали

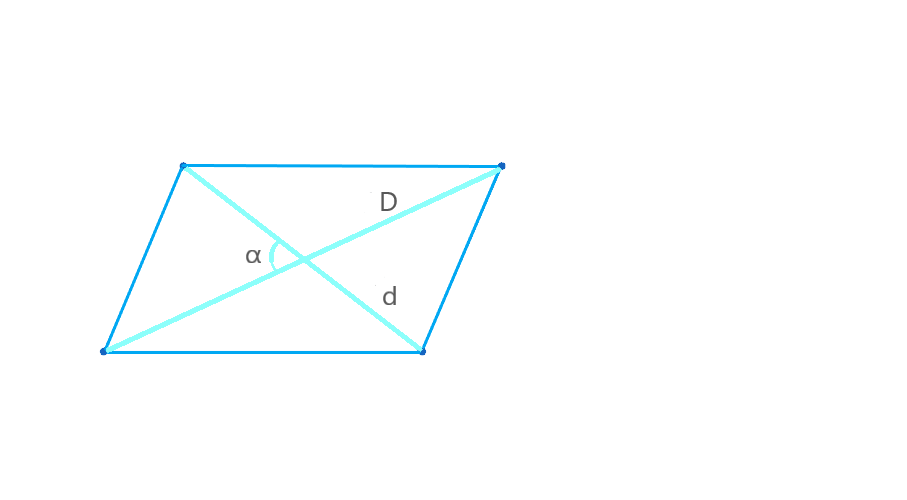
Площадь параллелограмма можно найти, если известны длины его диагоналей и угол между ними.

S = (d₁ × d₂ × sin(α)) / 2,

где:

• d₁ и d₂ — диагонали параллелограмма;
• α — угол между диагоналями.

Например, найдем площадь параллелограмма, у которого диагонали 10 см и 14 см, а угол между ними 75°.

Нам известно:

d₁ = 10 см,

d₂ = 14 см,

α = 75°.

Подставляем значения в формулу:

S = (10 × 14 × sin(75°)) / 2.

S ≈ (140 × 0,965) / 2.

S ≈ 135,1 / 2 ≈ 67,55 см².

Ответ: 67,55 см².

Задачи на нахождение площади

Рассмотрим три примера вычисления площади параллелограмма с разными исходными данными.

Задача 1

Найдите площадь параллелограмма, если его основание 9 см, а высота, проведенная к нему, равна 5 см.

Дано:

• a = 9 см
• h = 5 см

Для решения используем формулу:

S = a × h.

S = 9 × 5 = 45 см².

Ответ: 45 см².

Задача 2

Найдите площадь параллелограмма, если его стороны равны 7 см и 10 см, а угол между ними 45°.

Дано:

• a = 7 см
• b = 10 см
• α = 45°

Для решения используем формулу:

S = a × b × sin(α).

S = 7 × 10 × sin(45°).

S = 7 × 10 × 0,707.

S ≈ 49,49 см².

Ответ: 49,49 см².

Задача 3

Дан параллелограмм, диагонали которого равны 16 см и 12 см, а угол между ними 60°. Найдите его площадь.

Дано:

• d₁ = 16 см
• d₂ = 12 см
• α = 60°

Для решения используем формулу:

S = (d₁ × d₂ × sin(α)) / 2.

S = (16 × 12 × sin(60°)) / 2.

S = (192 × 0,866) / 2.

S ≈ 166,27 / 2 ≈ 83,14 см².

Ответ: 83,14 см².