Формула объема цилиндра

Объем цилиндра — это

Цилиндр — это геометрическое тело, которое образуется при вращении прямоугольника вокруг одной из его сторон.

В результате образуется фигура с двумя круглыми основаниями и боковой поверхностью.

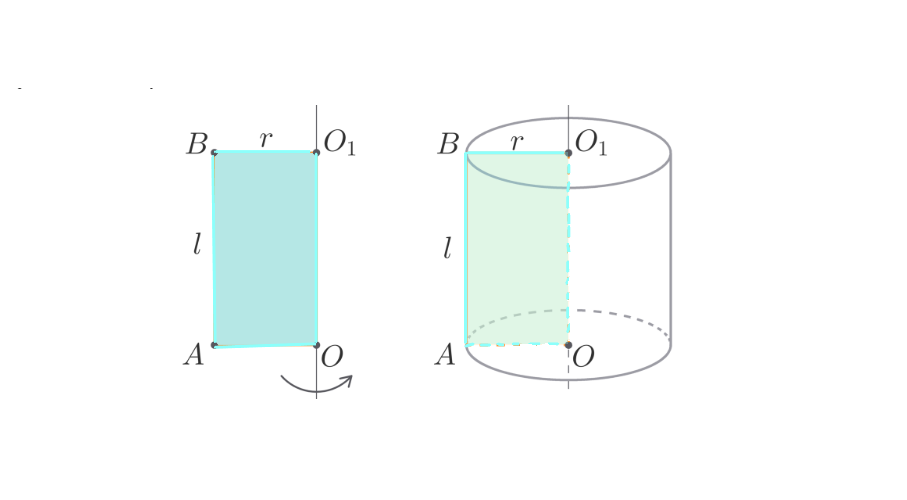
Цилиндр — это геометрическое тело, полученное при вращении прямоугольника вокруг одной из его сторон. У него есть несколько ключевых элементов.

• Ось цилиндра — прямая, вокруг которой вращался прямоугольник при его образовании. Она проходит через центры оснований и определяет направление фигуры.
• Основания цилиндра — два одинаковых круга, расположенные в параллельных плоскостях.
• Боковая поверхность (или цилиндрическая поверхность) — это внешняя часть цилиндра, соединяющая два основания.
• Образующие цилиндра — это отрезки, соединяющие соответствующие точки окружностей оснований. Они всегда параллельны оси цилиндра и лежат на боковой поверхности.
• Радиус цилиндра — это радиус одного из оснований. Он обозначается r и используется в формулах для вычисления площади и объема.
• Высота цилиндра — это расстояние между основаниями. Она измеряется вдоль перпендикуляра, опущенного из одной плоскости основания на другую, и обозначается h.

В прямом цилиндре образующие перпендикулярны основаниям, а в наклонном цилиндре — нет.

Для вычисления объема цилиндра используют формулу:

V = π × r² × h,

где:

• V — объем цилиндра;
• r — радиус основания;
• h — высота цилиндра;
• π ≈ 3,1416.

Например, найдем объем цилиндра, если радиус основания 5 см, а высота 10 см.

Решение:

Подставляем значения в формулу:

V = π × 5² × 10.

V = 3,1416 × 25 × 10.

V ≈ 785,4 см³.

Ответ: 785,4 см³.

Формула объема цилиндра по высоте и радиусу

Формула для вычисления объема цилиндра:

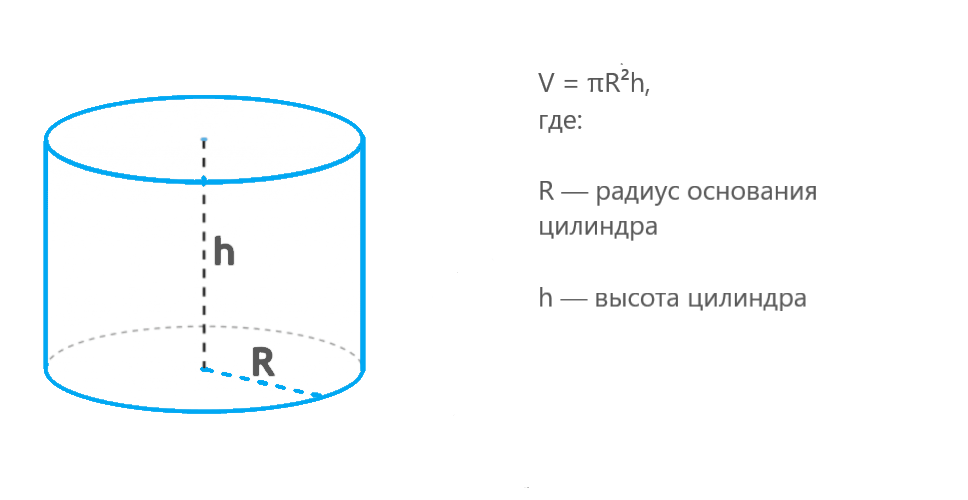
V = π × R² × h,

где:

• V — объем цилиндра;
• π — математическая константа (приблизительно 3,14159);
• R — радиус основания цилиндра;
• h — высота цилиндра.

Например, найдем объем цилиндра, если его радиус основания 4 см, а высота 10 см.

Для решения используем формулу:

V = π × R² × h.

Подставляем данные:

V = 3,14159 × 4² × 10.

V = 3,14159 × 16 × 10.

V ≈ 502,65 см³.

Ответ: 502,65 см³.

Объем цилиндра через площадь основания и высоту

Если известна площадь основания цилиндра, объем можно вычислить по формуле:

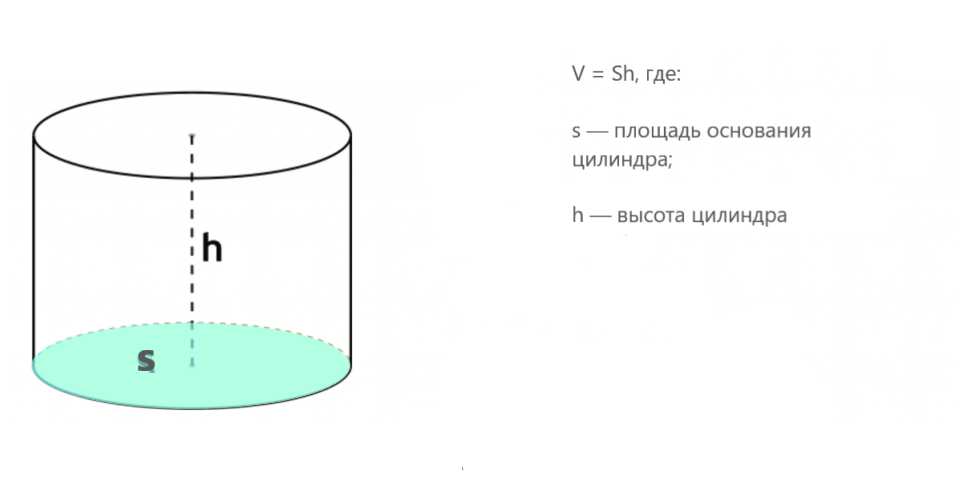
V = S × h,

где:

• V — объем цилиндра;
• S — площадь основания;
• h — высота цилиндра.

Площадь основания находится по формуле круга:

S = π × R²,

где R — радиус основания.

Например, найдем основание цилиндра имеет площадь 50 см², а его высота составляет 12 см. Найдите объем цилиндра.

Решение:

Используем формулу:

V = S × h.

Подставляем данные:

V = 50 × 12.

V = 600 см³.

Ответ: 600 см³.

Формула объема через высоту и диаметр

Формула для вычисления объема цилиндра, если известны его диаметр и высота:

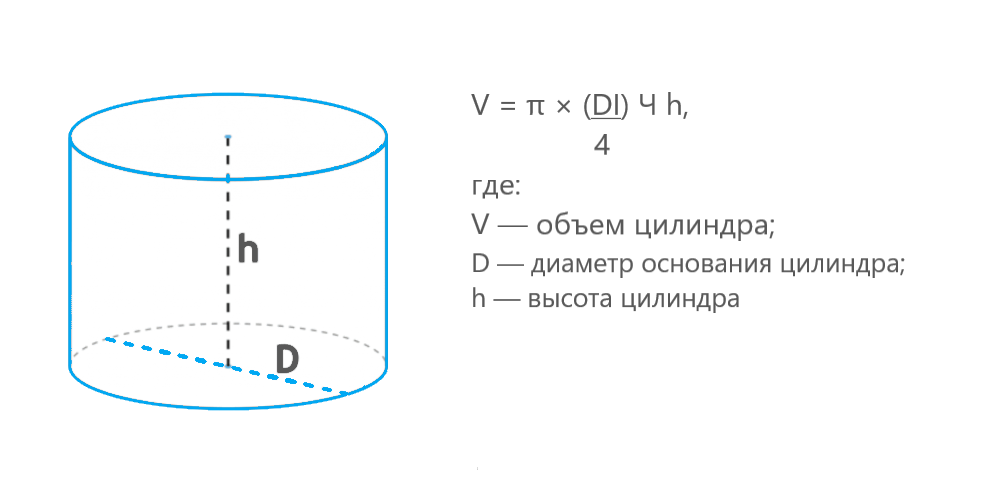
V = π × (D² / 4) × h,

где:

• V — объем цилиндра;
• π — математическая константа (примерно 3,14159);
• D — диаметр основания цилиндра;
• h — высота цилиндра.

Например, найдем объем цилиндра, если его диаметр основания 10 см, а высота 15 см.

Для решения используем формулу:

V = π × (D² / 4) × h.

Подставляем данные:

V = 3,14159 × (10² / 4) × 15.

V = 3,14159 × (100 / 4) × 15.

V = 3,14159 × 25 × 15.

V ≈ 1178,1 см³.

Ответ: 1178,1 см³.

Примеры решений задач на нахождение объема цилиндра

Пример 1

Условие:

Определить объем цилиндра, если радиус его основания R неизвестен, но известно, что высота h в 5 раз больше R.

Решение:

1. Обозначим радиус основания как R.
2. Высота цилиндра тогда будет h = 5R.
3. Используем формулу объема:
   
   V = π × R² × h.
4. Подставляем выражение для h:
   
   V = π × R² × (5R).
5. Получаем:
   
   V = 5π × R³.

Результат: объем выражен через R → V = 5π × R³. Если известно значение радиуса, можно сразу подставить и вычислить.

Пример 2

Условие:

Найти объем цилиндра, если радиус основания R = 17 см, а высота h = 140 см.

Для решения используем формулу:

V = π × R² × h.

Подставляем значения:

V = 3,14159 × 17² × 140.

V = 3,14159 × 289 × 140.

V ≈ 127 152,4 см³.

Ответ: 127 152,4 см³.

Пример 3

Условие:

Диаметр основания цилиндра равен 12 см, а высота 30 см. Найдите его объем.

Для решения используем формулу для объема через диаметр:

V = π × (D² / 4) × h.

Подставляем значения:

V = 3,14159 × (12² / 4) × 30.

V = 3,14159 × (144 / 4) × 30.

V = 3,14159 × 36 × 30.

V ≈ 3392,9 см³.

Ответ: 3392,9 см³.